Find the nth lucky number

Lucky number - It is the smallest integer for which m > 1. For a given positive integer n, pn# m is a prime number, where pn# is the first n product primes.
For example, to calculate the third lucky number, first calculate the product of the first 3 prime numbers (2, 3, 5), which is 30. Adding 2 gives us 32, which is an even number, and adding 3 gives us 33, which is a multiple of 3. Integers up to 6 can also be excluded. Adding 7 gives us 37, which is a prime number. Therefore, 7 is the third lucky number.
The lucky number for the first original number is -
3, 5, 7, 13, 23, 17, 19, 23, 37, 61, 67, 61, 71, 47, 107, 59, 61, 109….
Problem Statement
Given a number n. Find the nth lucky number.
Example 1
Input: n = 3
Output: 7
Explanation - Product of the first 3 price figures -
2 3 5 = 30 30 + 7 = 37, a prime number.
Example 2
Input: n = 7
Output: 19
Explanation - Product of the first 7 prime numbers -
2 3 5 7 11 13 17 = 510510 510510 + 19 = 510529, a prime number.
Method 1: Original method
A simple way to solve this problem is to first calculate pn#, the product of the first n prime numbers, and then find the difference between pn# and the next prime number. The difference obtained will be a lucky number.
pseudocode
procedure prime (num)
if num <= 1
ans = TRUE
end if
for i = 2 to sqrt(num)
if i is a factor of num
ans = false
end if
ans = true
end procedure
procedure nthFortunate (n)
prod = 1
count = 0
for i = 2 to count < n
if i is prime
prod = prod * i
count = count + 1
end if
nextPrime = prod + 2
while nextPrime is not prime
nextPrime = next Prime + 1
ans = nextPrime - prod
end procedure
Example: C implementation
In the following program, the lucky number is calculated by calculating the primitive of the first n prime numbers and finding the next prime number after the primitive. The lucky number is the difference between the next prime number and the primitive number.
#include <bits/stdc++.h>
using namespace std;
// Function to find if a number is prime or not
bool prime(unsigned long long int num){
if (num <= 1)
return true;
for (int i = 2; i <= sqrt(num); i++){
if (num % i == 0)
return false;
}
return true;
}
// Function to find the nth Fortunate number
unsigned long long int nthFortunate(int n){
long long int prod = 1, count = 0;
// Calculating product/primorial of first n prime numbers
for (int i = 2; count < n; i++){
if (prime(i)){
prod *= i;
count++;
}
}
// Find the next prime greater than the product of n prime numbers
unsigned long long int nextPrime = prod + 2;
while (!prime(nextPrime)){
nextPrime++;
}
// Fortunate number is the difference between prime and primorial
unsigned long long int ans = nextPrime - prod;
return ans;
}
int main(){
int n = 15;
cout << n << "th Fortunate number : " << nthFortunate(n);
return 0;
}
Output
15th Fortunate number : 107
Time complexity - O(nsqrt(n)), where the complexity of the prime() function is O(sqrt(n)), and the complexity of the for loop in nthFortunate() is O(nsqrt(n)) .
Space complexity - O(1)
Method 2: Sieve of Eratosthenes
The Sieve of Eratosthenes is used to bring all prime numbers up to a limit, which will give us a value MAX. In this method, we create a boolean array containing all true entries and mark all non-prime indexes as false. Then multiply the first n prime numbers in the array to get the product of the first n prime numbers. Then similarly to the previous method, start at 2 and add 1 to the product to get the next prime number. The difference between the next prime number and the product is the required lucky number.
pseudocode
procedure nthFortunate (n)
MAX is set
prime[MAX] = {true}
prime[0] = false
prime[1] = false
for i = 1 to i*i <= MAX
if prime[i]
for j = i*i to MAX with j = j + i in each iteration
prime [j] = false
end if
prod = 1
count = 0
for i = 2 to count < n
if prime[i]
prod = prod * i
count = count + 1
end if
nextPrime = prod + 2
while nextPrime is not prime
nextPrime = nextPrime + 1
ans = nextPrime - prod
end procedure
Example: C implementation
In the following program, a Boolean prime array of size MAX records all prime numbers before MAX. The original is then found by multiplying the first n prime numbers. Then similar to the previous method, find nextPrime. The difference between nextPrime and Product is the lucky number.
#include <bits/stdc++.h>
using namespace std;
// Function to find the nth Fortunate number
unsigned long long int nthFortunate(int n){
// Setting upper limit for Sieve of Eratosthenes
const unsigned long long int MAX = 1000000000;
vector<bool> prime(MAX, true);
prime[0] = prime[1] = false;
// Sieve of Eratosthenes to find all primes up to MAX
for (unsigned long long int i = 2; i * i <= MAX; i++){
if (prime[i]){
// Setting all the multiples of i to false
for (int j = i * i; j <= MAX; j += i){
prime[j] = false;
}
}
}
// Find the first n primes and calculate their product
unsigned long long int prod = 1, count = 0;
for (unsigned long long int i = 2; count < n; i++){
if (prime[i]){
prod *= i;
count++;
}
}
// Find next prime greater than product
unsigned long long int nextPrime = prod + 2;
while (!prime[nextPrime])
nextPrime++;
// Fortunate number is difference between prime and product
return nextPrime - prod;
}
int main(){
int n = 25;
cout << n << "th Fortunate number : " << nthFortunate(n);
return 0;
}
Output
15th Fortunate number : 107
Time complexity - O(n log(log(n)))
Space complexity - O(MAX)
in conclusion
To sum up, the nth lucky number can be found in the following two ways.
Elementary method: Find the product of the first n prime numbers, and calculate the next prime number based on the product. The difference between the prime number and the product is the nth lucky number.
Sieve of Eratosthenes: Find all prime numbers that reach a certain limit, and then calculate the product with the next prime number to find the lucky number.
Both methods are valid for smaller values of n simply due to variable size limitations. For larger values, more efficient and optimized solutions are required.
The above is the detailed content of Find the nth lucky number. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
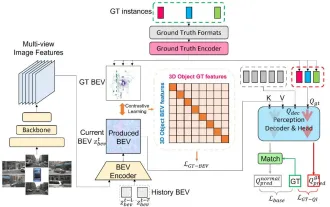 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 How to locate Apple wireless earphones if they are lost_How to locate Apple wireless earphones
Mar 23, 2024 am 08:21 AM
How to locate Apple wireless earphones if they are lost_How to locate Apple wireless earphones
Mar 23, 2024 am 08:21 AM
1. First, we open the [Search] App on the mobile phone and select the device in the list on the device interface. 2. Then, you can check the location and click on the route to navigate there.
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
 How to locate the other party's mobile phone location on Amap - How to locate the other party's mobile phone location on Amap
Apr 01, 2024 pm 02:11 PM
How to locate the other party's mobile phone location on Amap - How to locate the other party's mobile phone location on Amap
Apr 01, 2024 pm 02:11 PM
1. Click to enter the Amap map software on your mobile phone. 2. Click My in the lower right corner. 3. Click to enter the family map. 4. Click Create My Family Map. 5. After the creation is successful, an invitation code will appear and can be shared with another mobile phone.






