A relay spanning more than 300 years: Inspired by Terence Teru, mathematicians decided to use AI to formalize the proof of Fermat's Last Theorem.

Inspired by Terence Tao, more and more mathematicians are beginning to try to use artificial intelligence for mathematical exploration. This time, their target is Fermat's Last Theorem, one of the world's top ten most difficult mathematical problems. Fermat's Last Theorem is a very complex mathematical problem for which no feasible solution has been found so far. Mathematicians hope that with the help of artificial intelligence's powerful computing power and intelligent algorithms, they can explore in mathematics

Fermat's Last Theorem is also known as "Fermat's Last Theorem" Last Theorem (FLT)" was proposed by the 17th-century French mathematician Pierre de Fermat. There is a legendary story behind it. It is said that around 1637, when Fermat was reading the Latin translation of Diophantus' Arithmetic, he wrote next to Proposition 8 of Volume 11: "Divide a cubic number into the sum of two cubic numbers, or It is impossible to divide a fourth power into the sum of two fourth powers, or generally a power higher than the second power into the sum of two powers of the same power. "I am convinced that I have discovered something about this. This is a wonderful demonstration, but unfortunately the blank space here is too small to write it down. ”

What is stated before this paragraph is the content of Fermat’s last theorem: when the integer n>2, the equation about x^n y^n=z^n There is no positive integer solution.

Fermat said that he knew how to prove it, but because the blank part of the book was too small, he did not write about the authenticity of the story and whether Fermat really figured out the proof method. , it is controversial in later generations. For more than 300 years, mathematicians have been working hard to prove Fermat's last theorem. Until 1995, Professor Andrew Wiles of Princeton University in the United States spent 8 years. Working alone, Wiles finally completed the proof in 130 pages.

Now that Fermat's last theorem has been proved, mathematicians What else can you do with AI? The answer is: formalize its proofs.

Formalization in mathematics usually refers to the use of strict formal languages ​​(such as logic and set theory) to express mathematical objects, structures, Theorems and proofs enable them to be represented, verified and manipulated on computers, thereby ensuring the accuracy and consistency of mathematical content. The development of formal mathematics can be traced back to the late 19th and early 20th centuries, while modern formal mathematics The development of mathematical logic and computer science that began in the 20th century. The main goal of formal mathematics is to establish a formal system, which includes a set of symbols, a set of basic axioms and a set of reasoning rules. Through the application of these rules and axioms,

At the end of last year, Tao Zhexuan et al. Someone once used Lean (an interactive theorem prover and a programming language) to formalize one of their papers. The paper, a proof of a version of the polynomial Freiman-Ruzsa conjecture, was posted on arXiv last November. When writing Lean language code, Tao Zhexuan also used the AI ​​programming assistant Copilot. This incident attracted widespread attention in the mathematics and artificial intelligence communities.

At the time, Kevin Buzzard of Imperial College London, the most important promoter of the Lean technology open source community, said: "Fundamentally, it is obvious that when you digitize something, you can Use it in new ways. We will digitize mathematics, which will make mathematics better."

This is Professor Buzzard, the mathematician who recently claimed to formalize the proof of Fermat's last theorem. The tools are also Lean.

In a blog, he introduced the background, motivation and specific methods of doing this.

Why should we formalize the proof of Fermat’s Last Theorem?

The form of Fermat's Last Theorem is very simple and intuitive, but proving it is extremely difficult. This is undoubtedly an excellent demonstration of the profound beauty of mathematics. Over the past few centuries, in order to solve this problem, mathematicians have developed and innovated a large number of mathematical theories, which have applications in fields ranging from cryptography to physics.

Andrew Wiles may have been inspired by FLT, but his work actually led to a breakthrough in the Langlands Project, a series of far-reaching ideas in mathematics that linked number theory, algebraic geometry, and approximation. The theory of group representation is still attracting attention in 2024.

Historically, several other major breakthroughs in algebraic number theory (such as the theory of factorization in number fields and arithmetic in cyclic fields) were motivated at least in part by the desire for a deeper understanding of FLT.

Wiles' work, complemented by his student Richard Taylor, built on a vast foundation of 20th-century mathematics. The basic technique introduced by Wiles - the "modularity lifting theorem" - has been conceptually greatly simplified and widely generalized in the 30 years since the original paper was published. This field is still very active today. Frank Calegari's paper at the 2022 International Congress of Mathematicians, outlining progress since Wiles' breakthrough (see: https://arxiv.org/abs/2109.14145). Kevin Buzzard said that the continued activity in this field was one of his motivations for formalizing the FLT proof.

Formalization of mathematics is the art of converting mathematics on paper into a computer programming language that enables the understanding of theorems and proof concepts. These programming languages, also known as interactive theorem provers (ITPs), have been around for decades. In recent years, however, this area seems to have attracted some attention from the mathematical community. We have witnessed several examples of formalization of research in mathematics, the latest of which is the formalization of the proof of the polynomial Freiman-Ruzsa conjecture by Terence Tao and others. This 2023 breakthrough paper was formalized in Lean in just three weeks. Such success stories might lead onlookers to think that ITPs like Lean are now ready to formalize all modern mathematics.

However, the truth is far from simple. In some areas of mathematics, such as combinatorics, we can see some modern breakthroughs being formalized in real time. However, Buzzard said he regularly attended London number theory seminars and often noticed that Lean's knowledge of modern mathematical definitions was insufficient to formulate the results announced at the seminars, let alone verify their proofs.

In fact, the "lag" of number theory in this aspect was one of Buzzard's main motivations for launching the formalization of contemporary proofs of FLT. By the end of the project, Lean will be able to understand automorphic forms (a special class of functions of complex variables) and representations, Galois representations, latent automorphism, modularity promotion theorems, arithmetic of algebraic varieties, class field theory, arithmetic duals Theorems, Shimura varieties and other concepts used in modern algebraic number theory. In Buzzard's view, with these foundations in place, formalizing what's happening in his own area of ​​expertise will no longer be science fiction.

So, why do this? Buzzard explained, "If we believe some computer scientists, the exponential growth of artificial intelligence will eventually enable computers to help mathematicians in their research. Such work can help computers understand what we are doing in modern mathematical research."

How to carry out the project?

The formalization project of Fermat’s Last Theorem has now been launched. Buzzard shows current progress in a graphic.

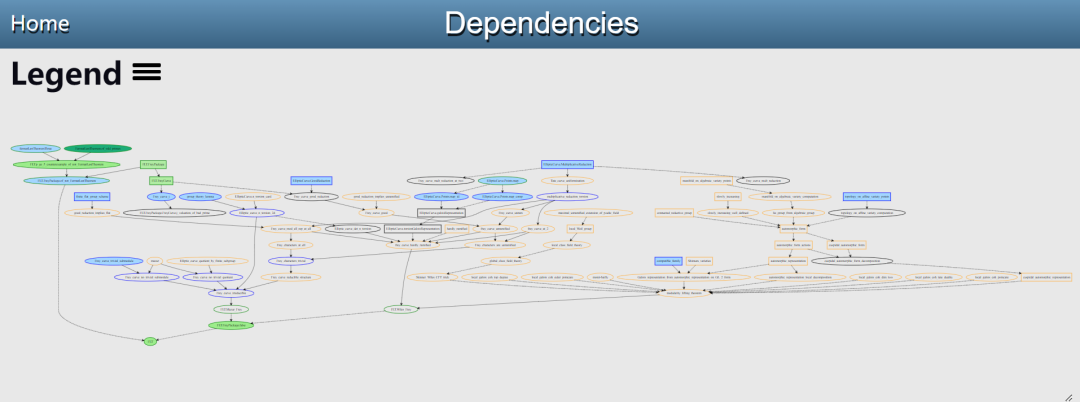
Interested researchers can read details: https://imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html

This project is sponsored by EPSRC funding will see Buzzard receive funding for the first five years. During this period, his first goal was to reduce FLT to a statement known to mathematicians in the late 1980s.

Of course, Buzzard had no intention of doing this alone. He said that for some parts of the argument, he understood the basic principles but had never examined the details in detail. Furthermore, Project Langlands also introduced some important things, including GL_2's cyclic basis transformation and Jacquet-Langlands. His understanding of these profound things is not deep enough.

However, this is precisely the advantage of formal projects. Buzzard will be able to articulate the results he needs in Lean and communicate them to others. The beauty of this system is: you don’t have to understand the entire proof of FLT to contribute. The diagram above breaks the proof into many small lemmas, making it very convenient for crowdsourcing. If you can formally prove any of these lemmas, Buzzard would eagerly await your pull request.

Those who want to participate in the project need to know something about Lean. For this, Buzzard recommends the online textbook Mathematics in Lean.

Textbook link: https://leanprover-community.github.io/mathematics_in_lean/

This project will be carried out on the FLT stream of Lean Zulip chat , a powerful research forum where mathematicians and computer scientists can collaborate in real time, easily publishing code and mathematics, using a thread and stream system to effectively support multiple independent conversations at the same time.

Lean Zulip chat link: https://leanprover.zulipchat.com/

Buzzard said he has no idea how long the project will take Premonition, but he's definitely optimistic.

At the same time, formal proof tools like Lean are also constantly iterating. Compared with the original Lean, the latest Lean 4 version has many optimizations, including a faster compiler, improved error handling, and better integration with external tools.

At the end of last year, the open platform LeanDojo team and researchers from the California Institute of Technology also launched Lean Copilot, a collaboration tool designed for large-scale language models to interact with humans, injecting AI into mathematical research. The power of big models.

"I predict that, if used correctly, AI will become a trusted co-author in mathematical research and many other fields by 2026." Tao Zhexuan said in a previous blog.

I hope Terence Tao’s prediction will come true soon.

Related reading:

• 《What is Terence Tao’s formal proof using AI? One article to understand the past and present life of PFR conjecture》

• 《Tao Zhexuan’s favored proof assistant Lean uses a large model》

• 《Large model helps Terence Tao solve problems and prove mathematical theorems: Is mathematics really going to become the first subject to achieve breakthroughs with the help of AI? 》

• ##《

  Tao Zhexuan’s new project: proving the prime number theorem in Lean, the research blueprint has been completed》

Reference link: https://leanprover.zulipchat.com/#narrow/stream/416277-FLT

https: //mp.weixin.qq.com/s/d9RSkRhlKH5ZMek3yTqe4Q

The above is the detailed content of A relay spanning more than 300 years: Inspired by Terence Teru, mathematicians decided to use AI to formalize the proof of Fermat's Last Theorem.. For more information, please follow other related articles on the PHP Chinese website!