Introduction to neural networks driven by physical information

Physical information-based neural network (PINN) is a method that combines physical models and neural networks. By integrating physical methods into neural networks, PINN can learn the dynamic behavior of nonlinear systems. Compared with traditional physical model-based methods, PINN has higher flexibility and scalability. It can adaptively learn complex nonlinear dynamic systems while meeting the requirements of physical specifications. This article will introduce the basic principles of PINN and provide some practical application examples.
The basic principle of PINN is to integrate physical methods into neural networks to learn the dynamic behavior of the system. Specifically, we can express the physical method in the following form:
F(u(x),\frac{\partial u}{\partial x},x,t) =0
Our goal is to understand the behavior of the system by learning the time evolution of the system state change u(x) and the boundary conditions around the system. To achieve this goal, we can use a neural network to simulate the development of the state change u(x) and use automatic differentiation techniques to calculate the gradient of the state change. At the same time, we can also use physical methods to constrain the relationship between the neural network and state changes. In this way, we can better understand the state evolution of the system and predict future changes.
Specifically, we can use the following loss function to train PINN:
L_{pinn}=L_{data} L_{ Physics}
where L_{data} is data loss, used to simulate the known state change value. Generally, we can use the mean square error to definitely define L_{data}:
L_{data}=\frac{1}{N}\sum_{i=1}^{ N}(u_i-u_{data,i})^2
where $N$ is the number of samples in the data set, u_i is the state change value predicted by the neural network, u_{data ,i} is the corresponding real state change value in the data set.
L_{physics} is the physical constraint loss, which is used to ensure that the neural network and state changes satisfy the physical method. In general, we can use the number of residuals to definitely define L_{physics}:
L_{physics}=\frac{1}{N}\sum_{i=1}^{ N}(F(u_i,\frac{\partial u_i}{\partial x},x_i,t_i))^2
where F is the physical method,\frac{\partial u_i}{\partial x} is the slope of the state change predicted by the neural network, x_i and t_i are the space and time coordinates similar to this i.
By minimizing L_{pinn}, we can simultaneously simulate data and satisfy physical methods, thereby learning the dynamic behavior of the system.
Now let’s look at some realistic PINN demonstrations. One typical example is learning the dynamic behavior of the Navier-Stokes method. The Navier-Stokes method describes the motion behavior of the fluid, which can be written in the following form:
\rho(\frac{\partial u}{\partial t} u\cdot\nabla u)=-\nabla p \mu\nabla^2u f
where \rho is the density of the fluid, u is the velocity of the fluid, p is the pressure of the fluid, \mu is the Density, f is the external force. Our goal is to learn the time evolution of the velocity and pressure of the fluid, as well as the boundary conditions at the fluid boundaries.
To achieve this goal, we can fill in the Navier-Stokes method into the neural network to facilitate learning the time evolution of speed and pressure. Specifically, we can use the following loss to train PINN:
L_{pinn}=L_{data} L_{physics}
The definitions of L_{data} and L_{physics} are the same as before. We can use a fluid dynamics model to generate a set of state variable data including velocity and pressure, and then use PINN to simulate state changes and satisfy the Navier-Stokes method. In this way, we can learn the dynamic behavior of flowing bodies, including phenomena such as wet flows, vortices, and boundary layers, without having to first determine a complex physical model or manually derive the analysis.
Another example is the kinematic behavior of learning nonlinear wave motion methods. The nonlinear wave motion method describes the propagation behavior of wave motion in the introduction, which can be written in the following form:
\frac{\partial^2u}{\partial t^2} -c^2\nabla^2u f(u)=0
where u is the amplitude of the wave speed, c is the wave speed, and f(u) is the item of nonlinear quality. Our goal is to learn the time evolution of the wave dynamics and boundary conditions at the introductory boundaries.
To achieve this goal, we can incorporate nonlinear wave processes into neural networks to facilitate learning of the epochal evolution of wave motion. Specifically, we can use the following damage numbers to train PINN:
L_{pinn}=L_{data} L_{physics}
The definitions of L_{data} and L_{physics} are the same as before. We can use numerical methods to generate a set of state change data containing amplitudes and steps, and then use PINN to simulate the state changes and satisfy the nonlinear wave method. In this way, we can study the time evolution of waves in a medium, including phenomena such as shape changes, refraction and reflection of wave packets, without first defining complex physical models or manually deriving the analysis.
In short, the neural network based on physical information is a method that combines physical models and neural networks, which can adapt to the earth's learning of complex non-linear dynamic systems while maintaining strict satisfaction of physical laws. PINN has been widely used in fluid mechanics, acoustics, structural mechanics and other fields, and has achieved some remarkable results. In the future, with the continuous development of neural networks and automated differential technology, PINN will hopefully become a larger, stronger and more versatile tool for solving various nonlinear dynamics problems.
The above is the detailed content of Introduction to neural networks driven by physical information. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
The bidirectional LSTM model is a neural network used for text classification. Below is a simple example demonstrating how to use bidirectional LSTM for text classification tasks. First, we need to import the required libraries and modules: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Explore the concepts, differences, advantages and disadvantages of RNN, LSTM and GRU
Jan 22, 2024 pm 07:51 PM
Explore the concepts, differences, advantages and disadvantages of RNN, LSTM and GRU
Jan 22, 2024 pm 07:51 PM
In time series data, there are dependencies between observations, so they are not independent of each other. However, traditional neural networks treat each observation as independent, which limits the model's ability to model time series data. To solve this problem, Recurrent Neural Network (RNN) was introduced, which introduced the concept of memory to capture the dynamic characteristics of time series data by establishing dependencies between data points in the network. Through recurrent connections, RNN can pass previous information into the current observation to better predict future values. This makes RNN a powerful tool for tasks involving time series data. But how does RNN achieve this kind of memory? RNN realizes memory through the feedback loop in the neural network. This is the difference between RNN and traditional neural network.
 Calculating floating point operands (FLOPS) for neural networks
Jan 22, 2024 pm 07:21 PM
Calculating floating point operands (FLOPS) for neural networks
Jan 22, 2024 pm 07:21 PM
FLOPS is one of the standards for computer performance evaluation, used to measure the number of floating point operations per second. In neural networks, FLOPS is often used to evaluate the computational complexity of the model and the utilization of computing resources. It is an important indicator used to measure the computing power and efficiency of a computer. A neural network is a complex model composed of multiple layers of neurons used for tasks such as data classification, regression, and clustering. Training and inference of neural networks requires a large number of matrix multiplications, convolutions and other calculation operations, so the computational complexity is very high. FLOPS (FloatingPointOperationsperSecond) can be used to measure the computational complexity of neural networks to evaluate the computational resource usage efficiency of the model. FLOP
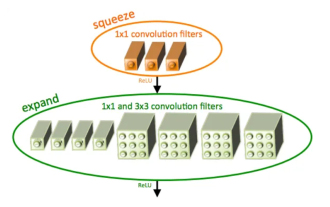 Introduction to SqueezeNet and its characteristics
Jan 22, 2024 pm 07:15 PM
Introduction to SqueezeNet and its characteristics
Jan 22, 2024 pm 07:15 PM
SqueezeNet is a small and precise algorithm that strikes a good balance between high accuracy and low complexity, making it ideal for mobile and embedded systems with limited resources. In 2016, researchers from DeepScale, University of California, Berkeley, and Stanford University proposed SqueezeNet, a compact and efficient convolutional neural network (CNN). In recent years, researchers have made several improvements to SqueezeNet, including SqueezeNetv1.1 and SqueezeNetv2.0. Improvements in both versions not only increase accuracy but also reduce computational costs. Accuracy of SqueezeNetv1.1 on ImageNet dataset
 Compare the similarities, differences and relationships between dilated convolution and atrous convolution
Jan 22, 2024 pm 10:27 PM
Compare the similarities, differences and relationships between dilated convolution and atrous convolution
Jan 22, 2024 pm 10:27 PM
Dilated convolution and dilated convolution are commonly used operations in convolutional neural networks. This article will introduce their differences and relationships in detail. 1. Dilated convolution Dilated convolution, also known as dilated convolution or dilated convolution, is an operation in a convolutional neural network. It is an extension based on the traditional convolution operation and increases the receptive field of the convolution kernel by inserting holes in the convolution kernel. This way, the network can better capture a wider range of features. Dilated convolution is widely used in the field of image processing and can improve the performance of the network without increasing the number of parameters and the amount of calculation. By expanding the receptive field of the convolution kernel, dilated convolution can better process the global information in the image, thereby improving the effect of feature extraction. The main idea of dilated convolution is to introduce some
 Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Convolutional neural networks perform well in image denoising tasks. It utilizes the learned filters to filter the noise and thereby restore the original image. This article introduces in detail the image denoising method based on convolutional neural network. 1. Overview of Convolutional Neural Network Convolutional neural network is a deep learning algorithm that uses a combination of multiple convolutional layers, pooling layers and fully connected layers to learn and classify image features. In the convolutional layer, the local features of the image are extracted through convolution operations, thereby capturing the spatial correlation in the image. The pooling layer reduces the amount of calculation by reducing the feature dimension and retains the main features. The fully connected layer is responsible for mapping learned features and labels to implement image classification or other tasks. The design of this network structure makes convolutional neural networks useful in image processing and recognition.
 Definition and structural analysis of fuzzy neural network
Jan 22, 2024 pm 09:09 PM
Definition and structural analysis of fuzzy neural network
Jan 22, 2024 pm 09:09 PM
Fuzzy neural network is a hybrid model that combines fuzzy logic and neural networks to solve fuzzy or uncertain problems that are difficult to handle with traditional neural networks. Its design is inspired by the fuzziness and uncertainty in human cognition, so it is widely used in control systems, pattern recognition, data mining and other fields. The basic architecture of fuzzy neural network consists of fuzzy subsystem and neural subsystem. The fuzzy subsystem uses fuzzy logic to process input data and convert it into fuzzy sets to express the fuzziness and uncertainty of the input data. The neural subsystem uses neural networks to process fuzzy sets for tasks such as classification, regression or clustering. The interaction between the fuzzy subsystem and the neural subsystem makes the fuzzy neural network have more powerful processing capabilities and can
 Twin Neural Network: Principle and Application Analysis
Jan 24, 2024 pm 04:18 PM
Twin Neural Network: Principle and Application Analysis
Jan 24, 2024 pm 04:18 PM
Siamese Neural Network is a unique artificial neural network structure. It consists of two identical neural networks that share the same parameters and weights. At the same time, the two networks also share the same input data. This design was inspired by twins, as the two neural networks are structurally identical. The principle of Siamese neural network is to complete specific tasks, such as image matching, text matching and face recognition, by comparing the similarity or distance between two input data. During training, the network attempts to map similar data to adjacent regions and dissimilar data to distant regions. In this way, the network can learn how to classify or match different data to achieve corresponding






