 Technology peripherals
Technology peripherals
 AI
AI
 What is the interaction principle between multidimensional tensors and linear layers?
What is the interaction principle between multidimensional tensors and linear layers?
What is the interaction principle between multidimensional tensors and linear layers?

Linear layer is one of the most commonly used layers in deep learning and plays an important role in neural networks. It is widely used in tasks such as image classification, object detection, and speech recognition. This article will focus on the role of linear layers on multi-dimensional tensors.
First, let’s review the basic principles of linear layers. For an input tensor The parameters of W are (n_out, n_in), and the shape of b is (n_out,). n_in represents the size of the input tensor, and n_out represents the size of the output tensor. Assume that the input tensor is a one-dimensional tensor x∈R^n_in, and the output tensor is also a one-dimensional tensor y∈R^n_out. In the linear layer, the input tensor is linearly transformed by the weight matrix W, plus the bias vector b, to obtain the output tensor y. This linear transformation can be expressed as y = Wx b. Among them, each row of W represents the weight vector of an output neuron of the linear layer, and each element of b represents the bias value of the corresponding output neuron. Each element of the final output tensor y is obtained by performing a dot product of the weight vector of the corresponding output neuron and the input tensor, plus the corresponding offset value.
Now, suppose we have a multi-dimensional tensor X whose shape is (n_1,n_2,…,n_k). We need to pass it to a linear layer to produce an output tensor Y with shape (m_1,m_2,…,m_l). At this time, what should we do?
First, we need to flatten X into a one-dimensional tensor. This process is often called a "levelling" operation and can be implemented using the view function in PyTorch. Specifically, we can change the shape of X to (n_1\times n_2\times...\times n_k,), that is, arrange the elements of all dimensions in one column. In this way, we get a one-dimensional tensor x, whose size is n_{in}=n_1\times n_2\times…\times n_k.
Next, we can pass x to the linear layer and get the output tensor y. Specifically, we can use the calculation formula of the linear layer:
y=Wx b
Here, the shape of W is (m_{out} ,n_{in}), the shape of b is (m_{out},), m_{out} represents the size of the output tensor. The result of multiplication Wx is a one-dimensional tensor with shape (m_{out},). After adding offset b, the output tensor y with shape (m_{out},) is obtained.
Finally, we need to convert y back to the form of a multidimensional tensor. Specifically, we can use the view function in PyTorch to change the shape of y to (m_1, m_2,...,m_l). In this way, we get the final output tensor Y.
It should be noted that when flattening a multi-dimensional tensor into a one-dimensional tensor, we need to ensure that the order of the elements in the tensor remains unchanged. For example, suppose we have a two-dimensional tensor X of shape (2,3):
X=\begin{bmatrix}1&2&3\4&5&6\end{bmatrix}
We need to flatten it into a one-dimensional tensor. If we use view(-1) to implement it, the result will be:
x=[1,2,3,4,5,6]
Here, we arrange the two rows of elements (1,2) and (4,5) together, causing the order to change. Therefore, the correct operation should be to use view(-1) to flatten the tensor, and then use view(1,-1) to convert it back to its original shape:
x =\begin{bmatrix}1&2&3&4&5&6\end{bmatrix}
##X=\begin{bmatrix}1&2&3\4&5&6\end{bmatrix} This way we can correctly pass the multidimensional tensor to the linear layer and get the correct output tensor. It should be noted that the role of a linear layer on a multi-dimensional tensor can be seen as an independent linear transformation for each sample. For example, suppose we have a four-dimensional tensor X with shape (N, C, H, W), where N represents the number of samples, C represents the number of channels, and H and W represent the height and width respectively. We can expand The linear layer performs an independent linear transformation on each sample to obtain an output tensor Y with a shape of (N,m_{out}). Finally, we can restore Y to its original shape (N,m_1,m_2,…,m_l) along the first dimension. In short, the role of a linear layer on a multi-dimensional tensor can be seen as an independent linear transformation for each sample. In practical applications, we usually flatten multi-dimensional tensors into one-dimensional tensors and pass them to linear layers. The flattening operation needs to ensure that the order of the elements remains unchanged, otherwise it will lead to incorrect calculation results. Finally, we need to restore the output tensor to its original shape for the next step of calculation.The above is the detailed content of What is the interaction principle between multidimensional tensors and linear layers?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 15 recommended open source free image annotation tools
Mar 28, 2024 pm 01:21 PM
15 recommended open source free image annotation tools
Mar 28, 2024 pm 01:21 PM
Image annotation is the process of associating labels or descriptive information with images to give deeper meaning and explanation to the image content. This process is critical to machine learning, which helps train vision models to more accurately identify individual elements in images. By adding annotations to images, the computer can understand the semantics and context behind the images, thereby improving the ability to understand and analyze the image content. Image annotation has a wide range of applications, covering many fields, such as computer vision, natural language processing, and graph vision models. It has a wide range of applications, such as assisting vehicles in identifying obstacles on the road, and helping in the detection and diagnosis of diseases through medical image recognition. . This article mainly recommends some better open source and free image annotation tools. 1.Makesens
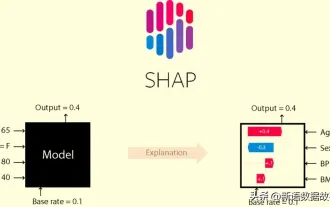 This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
In the fields of machine learning and data science, model interpretability has always been a focus of researchers and practitioners. With the widespread application of complex models such as deep learning and ensemble methods, understanding the model's decision-making process has become particularly important. Explainable AI|XAI helps build trust and confidence in machine learning models by increasing the transparency of the model. Improving model transparency can be achieved through methods such as the widespread use of multiple complex models, as well as the decision-making processes used to explain the models. These methods include feature importance analysis, model prediction interval estimation, local interpretability algorithms, etc. Feature importance analysis can explain the decision-making process of a model by evaluating the degree of influence of the model on the input features. Model prediction interval estimate
 Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves. Underfitting and overfitting 1. Overfitting If a model is overtrained on the data so that it learns noise from it, then the model is said to be overfitting. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score. Slightly modified: "Cause of overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set as a training set may not represent the correct representation of all data." 2. Underfitting Heru
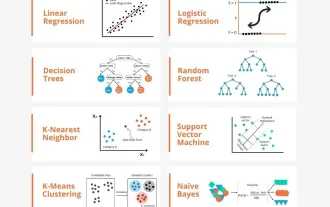 Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
In layman’s terms, a machine learning model is a mathematical function that maps input data to a predicted output. More specifically, a machine learning model is a mathematical function that adjusts model parameters by learning from training data to minimize the error between the predicted output and the true label. There are many models in machine learning, such as logistic regression models, decision tree models, support vector machine models, etc. Each model has its applicable data types and problem types. At the same time, there are many commonalities between different models, or there is a hidden path for model evolution. Taking the connectionist perceptron as an example, by increasing the number of hidden layers of the perceptron, we can transform it into a deep neural network. If a kernel function is added to the perceptron, it can be converted into an SVM. this one
 The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
In the 1950s, artificial intelligence (AI) was born. That's when researchers discovered that machines could perform human-like tasks, such as thinking. Later, in the 1960s, the U.S. Department of Defense funded artificial intelligence and established laboratories for further development. Researchers are finding applications for artificial intelligence in many areas, such as space exploration and survival in extreme environments. Space exploration is the study of the universe, which covers the entire universe beyond the earth. Space is classified as an extreme environment because its conditions are different from those on Earth. To survive in space, many factors must be considered and precautions must be taken. Scientists and researchers believe that exploring space and understanding the current state of everything can help understand how the universe works and prepare for potential environmental crises
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
May 30, 2024 pm 01:24 PM
Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
May 30, 2024 pm 01:24 PM
MetaFAIR teamed up with Harvard to provide a new research framework for optimizing the data bias generated when large-scale machine learning is performed. It is known that the training of large language models often takes months and uses hundreds or even thousands of GPUs. Taking the LLaMA270B model as an example, its training requires a total of 1,720,320 GPU hours. Training large models presents unique systemic challenges due to the scale and complexity of these workloads. Recently, many institutions have reported instability in the training process when training SOTA generative AI models. They usually appear in the form of loss spikes. For example, Google's PaLM model experienced up to 20 loss spikes during the training process. Numerical bias is the root cause of this training inaccuracy,
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing





