In-depth analysis of the concepts and applications of multiple linear regression models

Multiple linear regression is the most common form of linear regression and is used to describe how a single response variable Y exhibits a linear relationship with multiple predictor variables.

Examples of applications where multiple regression can be used:

The selling price of a house can be affected by factors such as location, number of bedrooms and bathrooms, year of construction, lot size, and more.

2. The height of a child depends on the height of the mother, the height of the father, nutrition and environmental factors.

Multiple linear regression model parameters

Consider a multiple linear regression model with k independent predictor variables x1, x2..., xk and a response variable y.

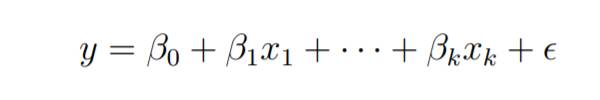
Suppose we have n observations for k 1 variables, and n variables should be greater than k.

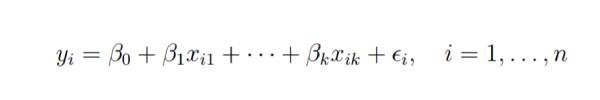
The basic goal of least squares regression is to fit the hyperplane into the (k 1)-dimensional space to minimize the sum of squared residuals .

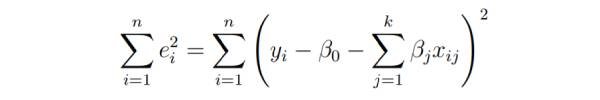
#Before differentiating the model parameters, set them to zero and derive the least squares normal equation that the parameters must satisfy.

These equations are formulated with the help of vectors and matrices.

The linear regression model is written as follows:

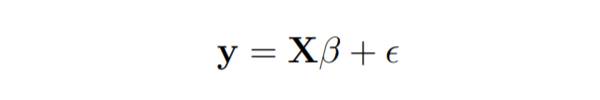
Online In linear regression, least squares parameter estimation b

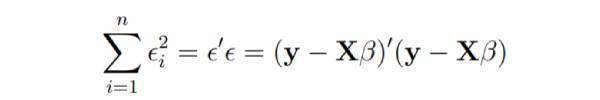
Imagine that the columns of changing. We wish to find the "best" b that minimizes the sum of squared residuals.

The smallest possible sum of squares is zero.

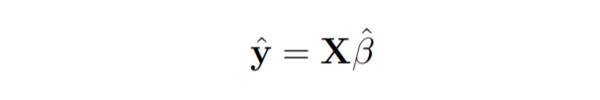
Here y is the estimated response vector.

The code implements multiple linear regression on the data set data2

data2 data set

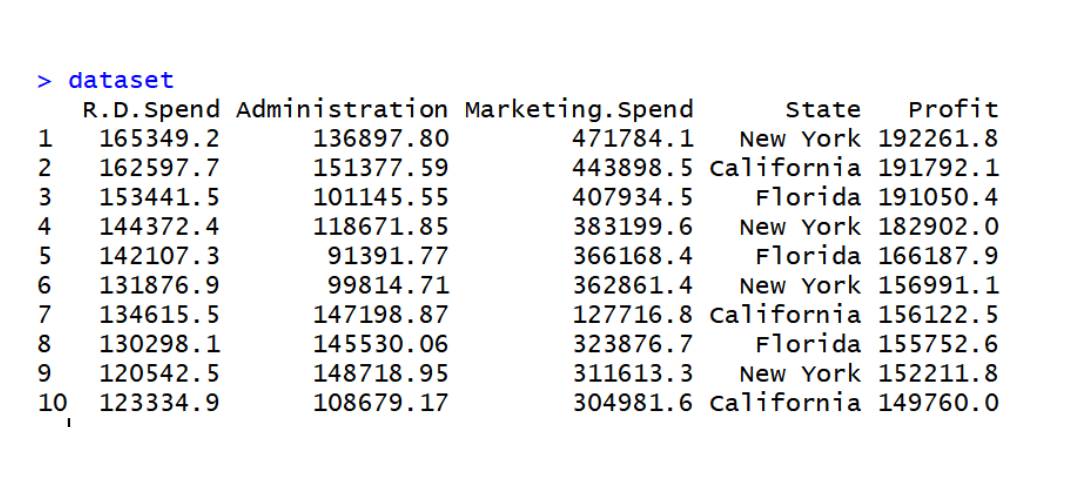
dataset=read.csv('data2.csv')
dataset$State=factor(dataset$State,
levels=c('New York','California','Florida'),
labels=c(1,2,3))
dataset$State

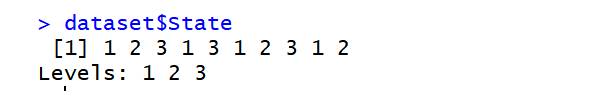
library(caTools)
set.seed(123)
split=sample.split(dataset$Profit,SplitRatio=0.8)
training_set=subset(dataset,split==TRUE)
test_set=subset(dataset,split==FALSE)
regressor=lm(formula=Profit~.,
data=training_set)
y_pred=predict(regressor,newdata=test_set)

The above is the detailed content of In-depth analysis of the concepts and applications of multiple linear regression models. For more information, please follow other related articles on the PHP Chinese website!