 Backend Development
Backend Development
 C++
C++
 Divide two integers without using the multiplication, division, and modulo operators
Divide two integers without using the multiplication, division, and modulo operators
Divide two integers without using the multiplication, division, and modulo operators

In this problem, we only need to divide two integers without using multiplication, division and modulo operators. Although we can use addition, multiplication or bit operations.
The problem statement states that we will get two integers x and y. Without using multiplication, division, or the modulo operator, we need to determine the quotient of x divided by y.
Example
Input: x=15, y=5
Output: 3
Input: x=10, y=4
Output: 2
Input: x=-20, y=3
Output:-6
method
Method 1 (Using Simple Math)
In this method, we will use a simple mathematical algorithm. Here are the step-by-step instructions for what we will follow -
We will continue to subtract the divisor (i.e. y) from the dividend (i.e. x) until x is greater than or equal to y.
When y is greater than x, that is, the divisor is greater than the dividend, the dividend becomes the remainder, and the number of subtractions becomes the quotient.
Store the number of times the subtraction is performed in a variable and return it, this is the output we want.
Example
The following is the C implementation of the above algorithm &minnus;
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
long long division(long long a,long long b) // where a is dividend and b is divisor
{
long long sign=1;
if((a<0) ^( b<0)) // - ^ - = +,+ ^ - = - , - ^ + = - , + ^ + = +
{
sign=-1;
}
long long m=abs(a);
long long n=abs(b);
long long count=0; // for storing the quotient
while(m>=n){
m=m-n;
count++;
}
if(sign==-1) // when sign is negative
{
count=-count;
}
return count;
}
int main(){
long long a=-21474;
long long b=2;
long long val=division(a,b);
cout<<val<<endl;
return 0;
}
Output
-10737
Time complexity: O(a/b)
Space complexity: O(1)
Method 2 (using bit operations)
Since any number can be represented in the form of 0 or 1, the quotient can be represented in binary form using the shift operator.
Use a for loop to iterate the bit positions of the divisor from 31 to 1.
Find the first bit where the divisor, that is, b<
When verifying the next position, add the result to the temp variable to ensure that temp (b<
Update the quotient each time by calculating the quotientOR 1<
Return to the quotient after updating the corresponding symbol.
Example
The following is the C implementation of the above method -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
long long division(long long a,long long b) // where a is dividend and b is divisor
{
long long sign=1;
if((a<0) ^( b<0)) // - ^ - = +,+ ^ - = - , - ^ + = - , + ^ + = +
{
sign=-1;
}
long long m=abs(a);
long long n=abs(b);
long long count=0; // for storing the quotient
long long temp=0;
for (int j = 31; j >= 0; --j){
if (temp + (n << j) <= m){
temp += n << j;
count |= 1L << j;
}
}
if(sign==-1) // when sign is negative
{
count=-count;
}
return count;
}
int main(){
long long a=49;
long long b=5;
long long val=division(a,b);
cout<<val<<endl;
a=-18,b=5;
cout<<division(a,b);
return 0;
}
Output
9 -3
Time complexity: O(log(a))
Space complexity: O(1), because it does not use extra space.
Method 3 (using logarithmic function)
In this method, we will use a simple logarithmic function to calculate the quotient.
As we all know,
$$\mathrm{In(\frac{a}{b})\:=\:In(a)\:-\:In(b)}$$
can be further modified to
$$\mathrm{\frac{a}{b}\:=\:e^{(In(a)\:-\:In(b))}}$$
So this is the basic idea to solve the given problem using this efficient method.
Below are step-by-step instructions for the method we will follow -
If one of them (i.e. dividend or divisor) is 0, we will return 0.
Now we will check the symbol using the exclusive OR function (XOR) to store the symbol in a variable.
If the divisor is 1, the dividend is returned directly.
Now, declare a variable and use the exp< 将等于 $\mathrm{e^{(In(a)\:-\:In(b))}}$ 的值存储在其中/b> function and the log function.
Log and exp are built-in functions in C. The log function returns the natural logarithm of the input number, and exp returns a value equal to e plus the input value.
Example
The following is the C implementation of the above method -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
long long int divide(long long int a,long long int b){
long long int sign=1;
if(a==0||b==0) // when a is zero or b is zero
{
return 0;
}
if((a>0) ^ (b>0)) // - ^ - = +,+ ^ - = - , - ^ + = - , + ^ + = +
{
sign=-1;
}
if(b==1) // when b is 1 then it will return a example 51/1 = 51
{
sign==-1?-a:a;
return a;
}
long long int m=abs(a);
long long int n=abs(b);
//log function return the logarithmic value of the entered value with base e i.e. natural log of the entered value
//exp function return the value equal to e^(entered value)
long long int ans =exp(log(m) - log(n)) + 0.0000000001;
// if it gives the value in decimal we will add from 0.0000000001 to account for accuracy errors
if(sign==-1) // when sign is negative return the negative ans
{
return -ans;
}
return ans;
}
int main(){
long long int ans=divide(47,-9);
cout<<ans<<endl;
return 0;
}
Output
-5
Time complexity: O(1), , because it takes constant time to perform this operation.
Space complexity: O(1), because it does not use extra space.
in conclusion
In this article, we learn to divide two integers without using multiplication, division, or modulo operators. We learned to solve problems in different ways with different efficiencies. They use simple mathematics, bit operations, and logarithmic functions. Among them, using the logarithmic function is the most efficient method because its time complexity is O(1), which is the smallest among all methods.
I hope this article helped you solve all the concepts regarding this topic.
The above is the detailed content of Divide two integers without using the multiplication, division, and modulo operators. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1659
1659
 14
14
 1415
1415
 52
52
 1310
1310
 25
25
 1258
1258
 29
29
 1232
1232
 24
24
 Divide two integers without using the multiplication, division, and modulo operators
Sep 21, 2023 pm 12:41 PM
Divide two integers without using the multiplication, division, and modulo operators
Sep 21, 2023 pm 12:41 PM
In this problem, we only need to divide two integers without using multiplication, division and modulo operators. Although we can use addition, multiplication or bit operations. The problem statement states that we will get two integers x and y. Without using multiplication, division, or the modulo operator, we need to determine the quotient of x divided by y. Example Input: x=15, y=5 Output: 3 Input: x=10, y=4 Output: 2 Input: x=-20, y=3 Output: -6 Method Method 1 (use simple math) here In this method, we will use a simple mathematical algorithm. Here is a step-by-step explanation of the steps we will follow - we will keep subtracting the divisor (i.e. y) from the dividend (i.e. x) until x is greater than or equal to y. when y is greater than x
 Oracle database operation skills: detailed explanation of subtraction operation
Mar 02, 2024 pm 06:15 PM
Oracle database operation skills: detailed explanation of subtraction operation
Mar 02, 2024 pm 06:15 PM
As a powerful relational database management system, Oracle database provides a wealth of computing operations to meet user needs. In daily database operations, subtraction operation is a common and important operation. It can help us realize the subtraction operation of data to obtain the results we need. This article will discuss in detail the techniques related to subtraction operations in Oracle database, and give specific code examples to help readers better understand and use this function. 1. Basic concepts of subtraction operations in Oracle data
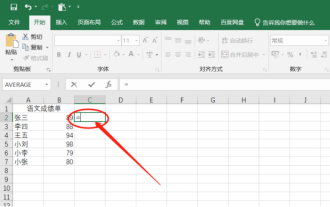 How to do subtraction in Excel
Mar 20, 2024 pm 02:46 PM
How to do subtraction in Excel
Mar 20, 2024 pm 02:46 PM
Excel is an indispensable office software in our daily office, so for some people who are learning Excel for the first time, they will always encounter some small problems, such as how to do subtraction in Excel. Today I will talk to my friends Share this operation step. The specific operation steps are below. Friends, come and take a closer look! 1. First, open the Excel data sheet. If Excel wants to do subtraction, it uses formulas, and formulas are generally guided by the equal sign. Therefore, in the cells that need to be subtracted, first enter =, (as shown in red below) Circled portion shown). 2. Then, click on the cell where the minuend is located, and the name of the cell will be automatically added to the formula (as shown in the red circle in the figure below). 3
 PHP exact division to get integer result
Apr 09, 2024 pm 01:09 PM
PHP exact division to get integer result
Apr 09, 2024 pm 01:09 PM
The division operator (/) in PHP performs floating-point division by default. If you need to get the integer result of the quotient, you can use the following method: floor() function: round down the integer (for example: floor(10.5)=10) ceil() Function: Round up an integer (for example: ceil(10.5)=11) Truncation operator (//): Truncate to an integer Modulo operator (%): Check whether the remainder is 0 to determine whether the result is an integer
 Explore the meaning and application of Python operators: addition, subtraction, multiplication and division
Jan 20, 2024 am 09:21 AM
Explore the meaning and application of Python operators: addition, subtraction, multiplication and division
Jan 20, 2024 am 09:21 AM
In-depth understanding of Python operators: addition, subtraction, multiplication, division and their meaning requires specific code examples. In the Python programming language, operators are one of the important tools for performing various mathematical operations. Among them, addition, subtraction, multiplication and division are the most common operators. This article will delve into the meaning of these operators and how to use them in Python. Addition Operator (+) The addition operator is used to add two numbers and can also be used to concatenate two strings. x=5y=3result
 How to make subtractive design and beautify charts in PPT
Mar 20, 2024 pm 02:00 PM
How to make subtractive design and beautify charts in PPT
Mar 20, 2024 pm 02:00 PM
1. The basic beautification operation space of the chart is small, and the interfering display elements are removed. Elements that interfere with the data include background, grid lines, and legends, which can be deleted, beautified, and shadows softened. 2. Enter [PPT], [Open] chart, click [Chart], select [+], and uncheck [check] it, as shown in the figure. 3. [Right-click] to set the format of the data series, click [Fill], and check [No Fill]. Click [Data Column], click [Shadow] to remove the shadow, select [Outline], and color [Text] white. 4. Click [Scale], select [Scale Mark], adjust [Theme Type] None, [Color] white, as shown in the figure. 5. Delete the places that need to be deleted to make the table clearer. Don’t blindly add things when designing, do it appropriately.
 Use pthread to implement matrix addition and subtraction in C/C++
Aug 28, 2023 am 09:05 AM
Use pthread to implement matrix addition and subtraction in C/C++
Aug 28, 2023 am 09:05 AM
Here we will see how to perform matrix addition and subtraction using a multi-threaded environment. pthread is used to execute multiple threads simultaneously in C or C++. There are two matrices A and B. The order of each matrix is (mxn). Each thread will get each row and perform addition or subtraction. So, for m rows, there are m different threads. Example#include<iostream>#include<pthread.h>#include<cstdlib>#include<cstdint>#defineCORE3#defineMAX3usingnamespacestd;i
 Use addition or subtraction to get the minimum number of steps for N at each step
Sep 16, 2023 pm 01:13 PM
Use addition or subtraction to get the minimum number of steps for N at each step
Sep 16, 2023 pm 01:13 PM
From the above problem statement, our task is to get the minimum number of steps in which the given number N can be obtained using addition or subtraction in each step. We can understand that we need to print the minimum number of steps that can be performed and the order of steps for any given integer N, by adding and subtracting step numbers to arrive at a number starting from 0. In this problem set, we can add or subtract a number equal to the number of steps to the current position at each step. For example, we can add 1 or -1 in step 1. Further we can add 2 or -2 in step 2 and so on. We can add or subtract numbers at each step depending on the situation. The main challenge of this problem is that we need to perform the minimum number of steps starting from 0 to reach N. Let us understand this question better through an example



