Add all larger values in the given binary search tree to each node

BST or Binary Search Tree is a form of binary tree in which the value of all left nodes is less than the value of the root node and the value of all right nodes is greater than the value of the root node. For this problem, we will take a binary tree and add to it all values greater than the current node value. The problem "add all larger values to each node of a BST" is simplified to, for a BST, add all node values larger than the current node value to that node value.
Add all larger values to each node in BST Problem Statement:
Given a Binary Search Tree (BST), we need to add all larger values to each node The sum of nodes.
Input
10
/ \
/ \
5 20
/ \ / \
1 7 1 5Output
70
/ \
82 45
/ \ / \
83 77 60 25Explanation
This program will convert a binary search tree into a binary tree where the node values are all The sum of the large elements plus the original value of the node.
Add all larger values to each node in the binary search tree solution:
We use reverse inorder traversal (recursively calling the right subtree first instead of the left subtree ), and maintains a variable to store the sum of nodes traversed so far.
We then use this sum to modify the value of the current node, first adding its value to the sum, and then replacing the node's value with this sum.
Example
#include <iostream >
using namespace std;
struct node {
int data;
node *left;
node *right;
};
node *newNode(int key) {
node *temp=new node;
temp->left=NULL;
temp->right=NULL;
temp->data=key;
return temp;
}
void Inorder(node *root) {
if(!root)
return;
Inorder(root->left);
cout<<root->data<<" ";
Inorder(root->right);
}
node *Insert(node *root,int key) {
if(!root)
return newNode(key);
if(key<root->data)
root->left=Insert(root->left,key);
else
root->right=Insert(root->right,key);
return root;
}
void RevInorderAdd(node *root,int &sum) {
if(!root)
return;
RevInorderAdd(root->right,sum);
sum+=root->data;
root->data=sum;
RevInorderAdd(root->left,sum);
}
void AddGreater(node *root) {
int sum=0;
RevInorderAdd(root,sum);
}
int main() {
/* Let us create following BST
10
/ \
5 20
/ \ / \
1 7 15 25 */
node *root = NULL;
root = Insert(root, 10);
Insert(root, 20);
Insert(root, 25);
Insert(root, 15);
Insert(root, 5);
Insert(root, 7);
Insert(root, 1);
Inorder(root);
cout<<endl;
AddGreater(root);
Inorder(root);
cout<<endl;
return 0;
}The above is the detailed content of Add all larger values in the given binary search tree to each node. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Query the minimum weight in the subtree starting from node X and distance at most D
Aug 25, 2023 am 11:25 AM
Query the minimum weight in the subtree starting from node X and distance at most D
Aug 25, 2023 am 11:25 AM
When doing computer programming, sometimes it is necessary to find the minimum weight of a subtree originating from a specific node, provided that the subtree cannot contain nodes that are more than D units away from the specified node. This problem arises in various fields and applications, including graph theory, tree-based algorithms, and network optimization. A subtree is a subset of a larger tree structure, with the specified node serving as the root node of the subtree. A subtree contains all descendants of the root node and their connecting edges. A node's weight refers to a specific value assigned to that node, which can represent its importance, significance, or other relevant metrics. In this problem, the goal is to find the minimum weight among all nodes in a subtree while limiting the subtree to nodes that are at most D units away from the root node. In the following article, we will delve into the complexity of mining minimum weights from subtrees
 C++ code to reverse paths in a binary search tree using queues
Sep 14, 2023 pm 07:21 PM
C++ code to reverse paths in a binary search tree using queues
Sep 14, 2023 pm 07:21 PM
For example, given a binary search tree, we need to reverse its path from a specific key. Ways to find the solution In this approach we will create a queue and push all the nodes until we get the root node. p>Example #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(intitem){&nb
 How to implement the node copy and cut functions of mind maps through Vue and jsmind?
Aug 15, 2023 pm 05:57 PM
How to implement the node copy and cut functions of mind maps through Vue and jsmind?
Aug 15, 2023 pm 05:57 PM
How to implement the node copy and cut functions of mind maps through Vue and jsmind? Mind map is a common thinking tool that can help us organize our thoughts and sort out our thinking logic. The node copy and cut functions are commonly used operations in mind maps, which allow us to reuse existing nodes more conveniently and improve the efficiency of thinking organization. In this article, we will use the two tools Vue and jsmind to implement the node copy and cut functions of the mind map. First, we need to install Vue and jsmind and create
 Binary heap and binary search tree in C++
Aug 22, 2023 pm 04:10 PM
Binary heap and binary search tree in C++
Aug 22, 2023 pm 04:10 PM
In C++ programming, binary heap and binary search tree are two commonly used data structures. They have similarities, but they also have differences. This article will introduce the concepts, basic operations and application scenarios of binary heaps and binary search trees respectively. 1. Binary Heap 1.1 Concept Binary heap is a complete binary tree that satisfies the following two properties: 1.1.1 Heap ordering Heap ordering means that in a binary heap, the value of each node is not greater than (or not less than) the value of its parent node. Here we take the maximum heap as an example, that is, the value of the root node is the largest value in the entire tree, and
 How to implement a binary search tree in Python
Jun 10, 2023 am 08:57 AM
How to implement a binary search tree in Python
Jun 10, 2023 am 08:57 AM
Binary Search Tree (BinarySearchTree, BST) is a search algorithm based on binary trees. Its characteristic is that the value in the left subtree of each node in the tree is smaller than the value of this node, while the value in the right subtree is greater than the value of this node. Therefore, the time complexity of BST search and insertion operations is O(logN). The method of implementing a binary search tree in Python is relatively simple, because Python has two built-in data structures, lists and dictionaries, both of which can be used to implement binary trees. At this
 What is the method to delete node in js
Sep 01, 2023 pm 05:00 PM
What is the method to delete node in js
Sep 01, 2023 pm 05:00 PM
The methods for deleting nodes in js are: 1. The removeChild() method is used to remove the specified child node from the parent node. It requires two parameters. The first parameter is the child node to be deleted, and the second parameter is the parent node. Node; 2. The parentNode.removeChild() method can be called directly through the parent node to delete the child node; 3. The remove() method can directly delete the node without specifying the parent node; 4. The innerHTML attribute is used to delete the node. content.
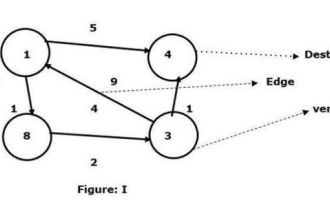 Find the shortest path between any two nodes using the Floyd-Warshal algorithm
Sep 20, 2023 pm 02:21 PM
Find the shortest path between any two nodes using the Floyd-Warshal algorithm
Sep 20, 2023 pm 02:21 PM
C++ has a macro, which is defined as a piece of code or an expected value, and it will be reused whenever the user needs it. The Floyd-Walshall algorithm is the process of finding the shortest path between all pairs of vertices in a given weighted graph. The algorithm follows a dynamic programming approach to find the minimum weight graph. Let us understand the meaning of Floyd-Walshall algorithm through a diagram - take vertex 1 as the source and vertex 4 as the destination and find the shortest path between them. We have seen that there are two paths that can be connected to the target vertex 4. 1->4 – the edge has a weight of 51->8->3->4 – the edge weight (1+2+1) is 4. In the given graph I, we see the smallest edge connecting two vertices. So here the vertex
 How to create, delete, append and replace element nodes in js (with code examples)
Aug 06, 2022 pm 05:26 PM
How to create, delete, append and replace element nodes in js (with code examples)
Aug 06, 2022 pm 05:26 PM
This article mainly introduces how to create, delete, append and replace element nodes in js. I hope it will be helpful to friends in need!






