 Backend Development
Backend Development
 C++
C++
 C program to calculate the area of a square within a circle inscribed in a hexagon
C program to calculate the area of a square within a circle inscribed in a hexagon
C program to calculate the area of a square within a circle inscribed in a hexagon

Given a square inscribed in a circle inscribed by a regular hexagon, we need to find the area of the square. To do this, we need to find the side length of the square and the sides of the regular hexagon. long relationship.
The mathematical formula for the radius of the inscribed circle of a regular hexagon is, r=A√3/2
Since the diagonal of the square is equal to the diameter of the circle, the distance between the radius and the side length The relationship is, a=√r
According to the side length of the regular hexagon,
a = √3A/√2
So, the area of the square, area=a2 = (√3A/√ 2)2
Example
#include <stdio.h>
#include <math.h>
int main() {
float a = 5;
float area = pow((a * sqrt(3)) / (sqrt(2)), 2);
printf("area = %f", area);
return 0;
}Output
area = 37.500000
The above is the detailed content of C program to calculate the area of a square within a circle inscribed in a hexagon. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Given below is a C language algorithm to convert Roman numerals to decimal numbers: Algorithm Step 1 - Start Step 2 - Read Roman numerals at runtime Step 3 - Length: = strlen(roman) Step 4 - For i=0 to Length-1 Step 4.1-switch(roman[i]) Step 4.1.1-case'm': &nbs
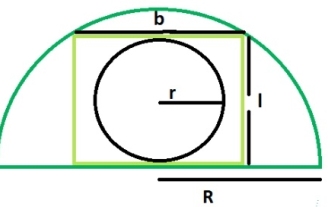 What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
A circle inscribed in a rectangle is tangent to the longer side of the rectangle, that is, its length is tangent to the circle. A rectangle inscribed in a semicircle touches two points on the arc of the semicircle. The width of the rectangle is equal to the diameter of the circle. If R is the radius of the semicircle. The length of the rectangle = √2R/2 The width of the rectangle = R/√2 The radius of the inscribed circle is r = b/2 = R/2√2 Using this formula we can calculate the rectangle inscribed in the semicircle The area of a circle, area = (π*r2)=π*R/8 Example Demonstration #include<stdio.h>intmain(){&
 Specific steps to create a hexagonal cluster layout in PPT
Mar 26, 2024 pm 03:21 PM
Specific steps to create a hexagonal cluster layout in PPT
Mar 26, 2024 pm 03:21 PM
1. First start PPT2010, execute the insert-picture command, insert a landscape picture material, and adjust the size. 2. Execute the insert command again, select smartart and then bring up the select smartart graphics dialog box. 3. Switch to the Picture tab, select the hexagonal cluster, and click the OK button to view the effect. 4. Then execute the Format-Add Shape command and click multiple times to add. Of course, adding shapes should be based on your actual situation. 5. Select the hexagon cluster and execute the Design-Convert-Convert to Shape command to convert it into a graphic. 6. Select the image to execute the Cut command, right-click the shape and select the Format Shape command from the drop-down menu. 7. In the Format Shape dialog box, set the fill to a picture or texture.
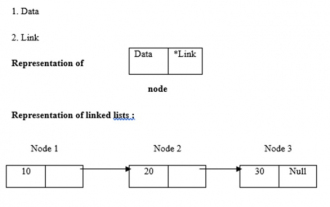 C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
Linked lists use dynamic memory allocation, i.e. they grow and shrink accordingly. They are defined as collections of nodes. Here, a node has two parts, data and links. The representation of data, links and linked lists is as follows - Types of linked lists There are four types of linked lists, as follows: - Single linked list/Singly linked list Double/Doubly linked list Circular single linked list Circular double linked list We use the recursive method to find the length of the linked list The logic is -intlength(node *temp){ if(temp==NULL) returnl; else{&n
 C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
Hyperbolic functions are defined using hyperbolas instead of circles and are equivalent to ordinary trigonometric functions. It returns the ratio parameter in the hyperbolic sine function from the supplied angle in radians. But do the opposite, or in other words. If we want to calculate an angle from a hyperbolic sine, we need an inverse hyperbolic trigonometric operation like the hyperbolic inverse sine operation. This course will demonstrate how to use the hyperbolic inverse sine (asinh) function in C++ to calculate angles using the hyperbolic sine value in radians. The hyperbolic arcsine operation follows the following formula -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Where\:In\:is\:natural logarithm\:(log_e\:k)
 C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
The rename function changes a file or directory from its old name to its new name. This operation is similar to the move operation. So we can also use this rename function to move files. This function exists in the stdio.h library header file. The syntax of the rename function is as follows: intrename(constchar*oldname,constchar*newname); The function of the rename() function accepts two parameters. One is oldname and the other is newname. Both parameters are pointers to constant characters that define the old and new names of the file. Returns zero if the file was renamed successfully; otherwise, returns a nonzero integer. During a rename operation
 C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
A map is a special type of container in C++ in which each element is a pair of two values, namely a key value and a map value. The key value is used to index each item, and the mapped value is the value associated with the key. Regardless of whether the mapped value is unique, the key is always unique. To print map elements in C++ we have to use iterator. An element in a set of items is indicated by an iterator object. Iterators are primarily used with arrays and other types of containers (such as vectors), and they have a specific set of operations that can be used to identify specific elements within a specific range. Iterators can be incremented or decremented to reference different elements present in a range or container. The iterator points to the memory location of a specific element in the range. Printing a map in C++ using iterators First, let's look at how to define
 C++ program to get the imaginary part of a given complex number
Sep 06, 2023 pm 06:05 PM
C++ program to get the imaginary part of a given complex number
Sep 06, 2023 pm 06:05 PM
Modern science relies heavily on the concept of plural numbers, which was first established in the early 17th century by Girolamo Cardano, who introduced it in the 16th century. The formula for complex numbers is a+ib, where a holds the html code and b is a real number. A complex number is said to have two parts: the real part <a> and the imaginary part (<ib>). The value of i or iota is √-1. The plural class in C++ is a class used to represent complex numbers. The complex class in C++ can represent and control several complex number operations. Let's take a look at how to represent and control the display of plural numbers. imag() member function As mentioned above, complex numbers are composed of real part and imaginary part. To display the real part we use real()





