Learn Python to solve advanced mathematics problems
Python solves advanced mathematics problems, and my mother no longer has to worry about my learning

Use Python to solve limits and derivatives in advanced mathematics , partial derivatives, definite integrals, indefinite integrals, double integrals and other problems
Sympy is a Python scientific computing library, which aims to become a fully functional computer algebra system. SymPy includes functions from basic symbolic arithmetic to calculus, algebra, discrete mathematics and quantum physics. It can display the results in LaTeX.
Sympy official website
Article directory
- Python solves advanced mathematics problems, my mother no longer has to worry about my study
- 1. Practical skills
- 1.1 Symbolic function
- 1.2 Expansion expression expand
- 1.3 Taylor expansion formula series
- 1.4 Sign expansion
- 2. Find the limit limit
- 3. Find the derivative diff
- 3.1 Unary function
- 3.2 Multivariate function
- 4. Integral integrate
- 4.1 Definite integral
- 4.2 Indefinite integral
- 4.3 Double integral
- 5. Solve the system of equations solve
- 6. Calculate the summation
(Free Learning recommendation: python video tutorial)

Watch Looking at this picture, do you feel like you can't breathe? Python is here to help you solve it.
from sympy import *import sympy
Enter the "x= symbols("x")" command to define a symbol
x = Symbol("x")y = Symbol("y")1. Practical tips
1.1 Symbol function
sympy provides a lot of mathematical symbols, summarized as follows
- Imaginary unit
sympy.I
- Natural logarithm
sympy.E
- Infinity
sympy.oo
- Pi
sympy.pi
- Find the nth square root
sympy.root(8,3)
- Get the logarithm
sympy.log(1024,2)
- Find the factorial
sympy.factorial(4)
- Trigonometric function
sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)
1.2 Expand expression expand
f = (1+x)**3expand(f)
x 3 + 3 x 2 + 3 x + 1 \displaystyle x^{3} + 3 x^{2} + 3 x + 1 x3+3x2+3x+1
1.3 泰勒展开公式series
ln(1+x).series(x,0,4)
x − x 2 2 + x 3 3 + O ( x 4 ) \displaystyle x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + O\left(x^{4}\right) x−2x2 3x3 O(x4)
sin(x).series(x,0,8)
x − x 3 6 + x 5 120 − x 7 5040 + O ( x 8 ) \displaystyle x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} + O\left(x^{8}\right) x−6x3 120x5−5040x7 O(x8)
cos(x).series(x,0,9)
1 − x 2 2 + x 4 24 − x 6 720 + x 8 40320 + O ( x 9 ) \displaystyle 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} + \frac{x^{8}}{40320} + O\left(x^{9}\right) 1−2x2 24x4−720x6 40320x8 O(x9)
(1/(1+x)).series(x,0,5)
1 − x + x 2 − x 3 + x 4 + O ( x 5 ) \displaystyle 1 - x + x^{2} - x^{3} + x^{4} + O\left(x^{5}\right) 1−x x2−x3 x4 O(x5)
tan(x).series(x,0,4)
x + x 3 3 + O ( x 4 ) \displaystyle x + \frac{x^{3}}{3} + O\left(x^{4}\right) x+3x3+O(x4)
(1/(1-x)).series(x,0,4)
1 + x + x 2 + x 3 + O ( x 4 ) \displaystyle 1 + x + x^{2} + x^{3} + O\left(x^{4}\right) 1+x+x2+x3+O(x4)
(1/(1+x)).series(x,0,4)
1 − x + x 2 − x 3 + O ( x 4 ) \displaystyle 1 - x + x^{2} - x^{3} + O\left(x^{4}\right) 1−x+x2−x3+O(x4)
1.4 符号展开
a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)x a + b \displaystyle x^{a + b} xa+b
2. 求极限limit
limit(sin(x)/x,x,0)
1 \displaystyle 1 1
f2=(1+x)**(1/x)
f2
( x + 1 ) 1 x \displaystyle \left(x + 1\right)^{\frac{1}{x}} (x+1)x1
重要极限
f1=sin(x)/x f2=(1+x)**(1/x)f3=(1+1/x)**x lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)
1 E E
dir可以表示极限的趋近方向
f4 = (1+exp(1/x))f4
e 1 x + 1 \displaystyle e^{\frac{1}{x}} + 1 ex1+1
lim4 = limit(f4,x,0,dir="-")lim4
1 \displaystyle 1 1
lim5 = limit(f4,x,0,dir="+")lim5
∞ \displaystyle \infty ∞
3. 求导diff
diff(函数,自变量,求导次数)
3.1 一元函数
求导问题
diff(sin(2*x),x)
2 cos ( 2 x ) \displaystyle 2 \cos{\left(2 x \right)} 2cos(2x)
diff(ln(x),x)
1 x \displaystyle \frac{1}{x} x1
3.2 多元函数
求偏导问题
diff(sin(x*y),x,y)
− x y sin ( x y ) + cos ( x y ) \displaystyle - x y \sin{\left(x y \right)} + \cos{\left(x y \right)} −xysin(xy)+cos(xy)
4. 积分integrate
4.1 定积分
- 函数的定积分: integrate(函数,(变量,下限,上限))
- 函数的不定积分: integrate(函数,变量)
f = x**2 + 1integrate(f,(x,-1.1))
− 1.54366666666667 \displaystyle -1.54366666666667 −1.54366666666667
integrate(exp(x),(x,-oo,0))
1 \displaystyle 1 1
4.2 不定积分
f = 1/(1+x*x)integrate(f,x)
atan ( x ) \displaystyle \operatorname{atan}{\left(x \right)} atan(x)
4.3 双重积分
f = (4/3)*x + 2*y integrate(f,(x,0,1),(y,-3,4))
11.6666666666667 \displaystyle 11.6666666666667 11.6666666666667
5. 求解方程组solve
#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])
{x: -1, y: 4}
6. 计算求和式summation
计算求和式可以使用sympy.summation函数,其函数原型为sympy.summation(f, *symbols, **kwargs)
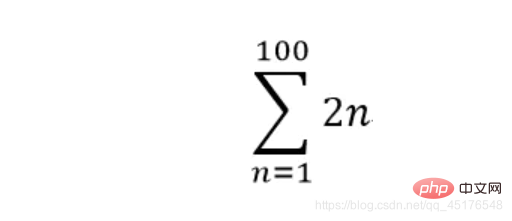
**
sympy.summation(2 * n,(n,1,100))
10100
到这里就结束了,如果对你有帮助,欢迎点赞关注评论,你的点赞对我很重要。在此也祝愿大家可以把数学学好
相关免费学习推荐:python教程(视频)
The above is the detailed content of Learn Python to solve advanced mathematics problems. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP is mainly procedural programming, but also supports object-oriented programming (OOP); Python supports a variety of paradigms, including OOP, functional and procedural programming. PHP is suitable for web development, and Python is suitable for a variety of applications such as data analysis and machine learning.
 Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
PHP is suitable for web development and rapid prototyping, and Python is suitable for data science and machine learning. 1.PHP is used for dynamic web development, with simple syntax and suitable for rapid development. 2. Python has concise syntax, is suitable for multiple fields, and has a strong library ecosystem.
 Python vs. JavaScript: The Learning Curve and Ease of Use
Apr 16, 2025 am 12:12 AM
Python vs. JavaScript: The Learning Curve and Ease of Use
Apr 16, 2025 am 12:12 AM
Python is more suitable for beginners, with a smooth learning curve and concise syntax; JavaScript is suitable for front-end development, with a steep learning curve and flexible syntax. 1. Python syntax is intuitive and suitable for data science and back-end development. 2. JavaScript is flexible and widely used in front-end and server-side programming.
 PHP and Python: A Deep Dive into Their History
Apr 18, 2025 am 12:25 AM
PHP and Python: A Deep Dive into Their History
Apr 18, 2025 am 12:25 AM
PHP originated in 1994 and was developed by RasmusLerdorf. It was originally used to track website visitors and gradually evolved into a server-side scripting language and was widely used in web development. Python was developed by Guidovan Rossum in the late 1980s and was first released in 1991. It emphasizes code readability and simplicity, and is suitable for scientific computing, data analysis and other fields.
 Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
VS Code can run on Windows 8, but the experience may not be great. First make sure the system has been updated to the latest patch, then download the VS Code installation package that matches the system architecture and install it as prompted. After installation, be aware that some extensions may be incompatible with Windows 8 and need to look for alternative extensions or use newer Windows systems in a virtual machine. Install the necessary extensions to check whether they work properly. Although VS Code is feasible on Windows 8, it is recommended to upgrade to a newer Windows system for a better development experience and security.
 Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
VS Code can be used to write Python and provides many features that make it an ideal tool for developing Python applications. It allows users to: install Python extensions to get functions such as code completion, syntax highlighting, and debugging. Use the debugger to track code step by step, find and fix errors. Integrate Git for version control. Use code formatting tools to maintain code consistency. Use the Linting tool to spot potential problems ahead of time.
 How to run python with notepad
Apr 16, 2025 pm 07:33 PM
How to run python with notepad
Apr 16, 2025 pm 07:33 PM
Running Python code in Notepad requires the Python executable and NppExec plug-in to be installed. After installing Python and adding PATH to it, configure the command "python" and the parameter "{CURRENT_DIRECTORY}{FILE_NAME}" in the NppExec plug-in to run Python code in Notepad through the shortcut key "F6".
 Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
VS Code extensions pose malicious risks, such as hiding malicious code, exploiting vulnerabilities, and masturbating as legitimate extensions. Methods to identify malicious extensions include: checking publishers, reading comments, checking code, and installing with caution. Security measures also include: security awareness, good habits, regular updates and antivirus software.






