Use Python to write the deletion operation code of B+ tree

B The tree deletion operation requires first finding the location of the deleted node, and then determining the number of keys of the node.

If the number of keys in the node exceeds the minimum number, just delete it directly.

As shown below, delete "40":

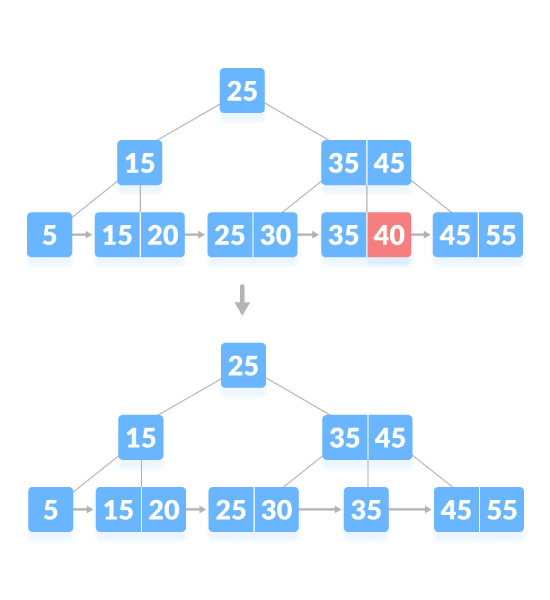
If there is an exact minimum number of keys in the node, deletion requires borrowing from the sibling node and adding the intermediate key of the sibling node to parent node. As shown below, delete "5":

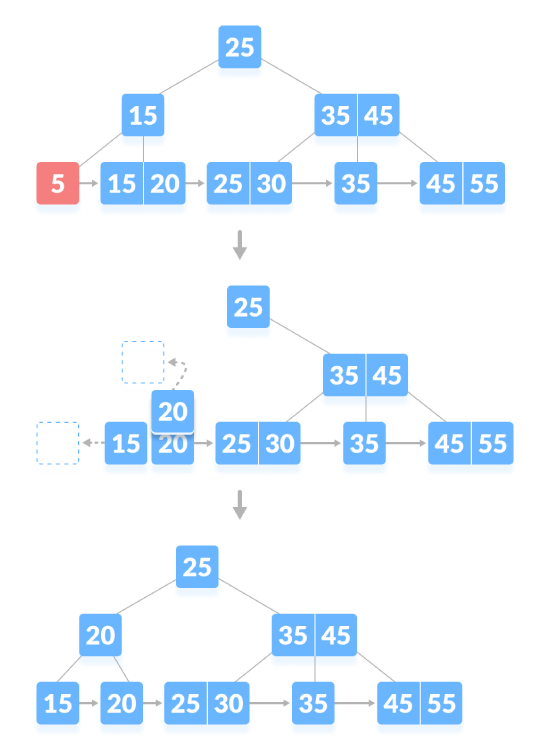
Delete the content node. If the number of keys in the node exceeds the minimum number, just delete it from the leaf node the key and delete the key from the internal node. Fill empty spaces in internal nodes with inorder successors. As shown below, delete "45":

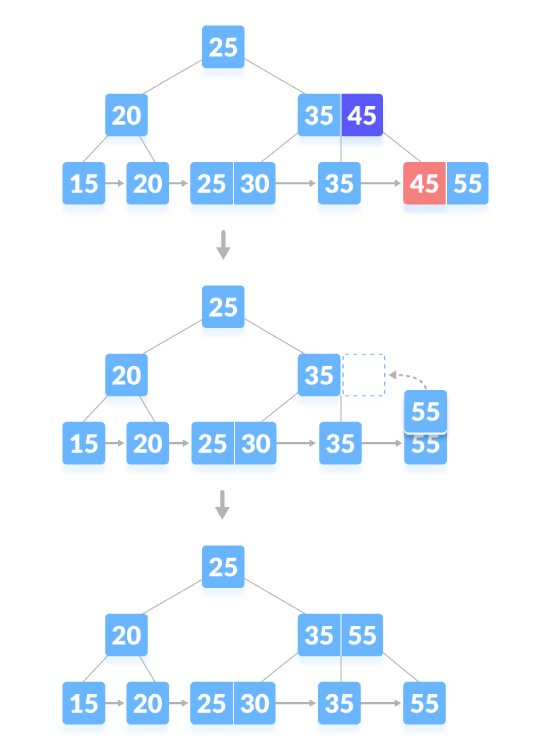
Delete the content node. If there is the exact minimum number of keys in the node, delete the key and directly The sibling borrows a key and fills the empty space in the index with the borrowed key. As shown below, delete "35":

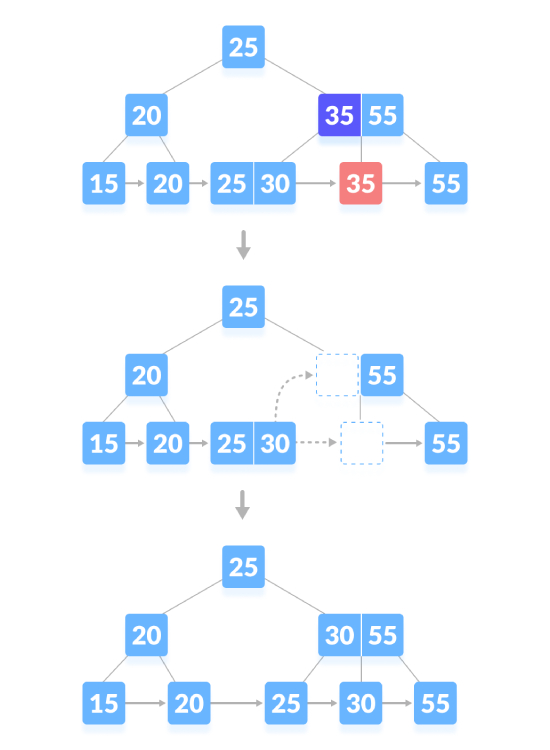
Delete the content node and generate a blank space above the parent node. After deleting a key, merge the empty space with its siblings, filling the empty space in the parent node with the inorder successor. As shown below, delete "25":

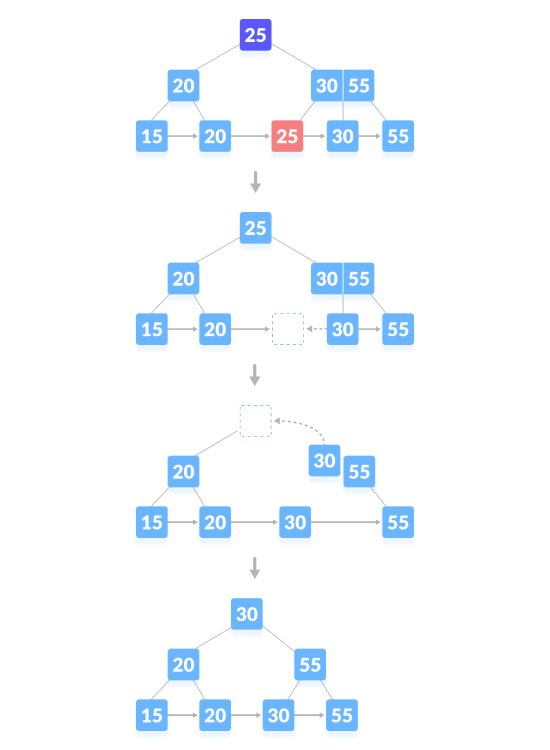
The deletion operation that causes the tree height to shrink, as shown below, delete "55":

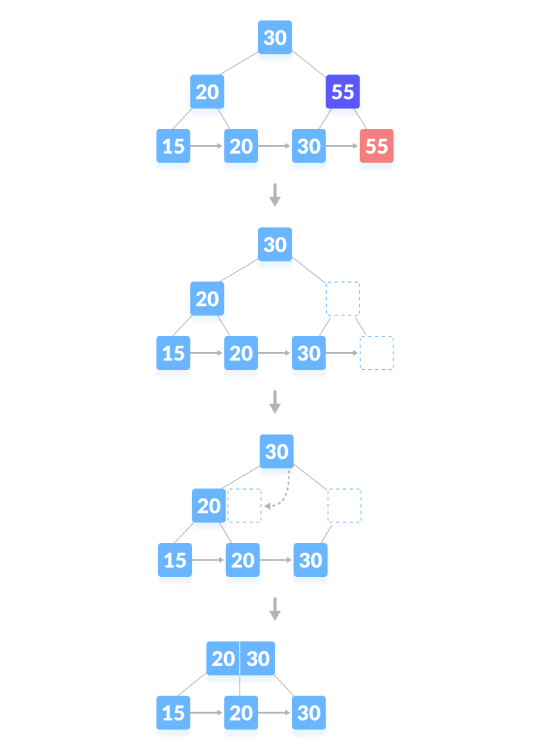
Python implements B-tree deletion operation

import math
# 创建节点
class Node:
    def __init__(self, order):
        self.order = order
        self.values = []
        self.keys = []
        self.nextKey = None
        self.parent = None
        self.check_leaf = False

# 插入叶子
    def insert_at_leaf(self, leaf, value, key):
        if (self.values):
            temp1 = self.values
            for i in range(len(temp1)):
                if (value == temp1[i]):
                    self.keys[i].append(key)
                    break
                elif (value < temp1[i]):
                    self.values = self.values[:i] + [value] + self.values[i:]
                    self.keys = self.keys[:i] + [[key]] + self.keys[i:]
                    break
                elif (i + 1 == len(temp1)):
                    self.values.append(value)
                    self.keys.append([key])
                    break
        else:
            self.values = [value]
            self.keys = [[key]]


# B+树
class BplusTree:
    def __init__(self, order):
        self.root = Node(order)
        self.root.check_leaf = True

    # 插入节点
    def insert(self, value, key):
        value = str(value)
        old_node = self.search(value)
        old_node.insert_at_leaf(old_node, value, key)

        if (len(old_node.values) == old_node.order):
            node1 = Node(old_node.order)
            node1.check_leaf = True
            node1.parent = old_node.parent
            mid = int(math.ceil(old_node.order / 2)) - 1
            node1.values = old_node.values[mid + 1:]
            node1.keys = old_node.keys[mid + 1:]
            node1.nextKey = old_node.nextKey
            old_node.values = old_node.values[:mid + 1]
            old_node.keys = old_node.keys[:mid + 1]
            old_node.nextKey = node1
            self.insert_in_parent(old_node, node1.values[0], node1)

    def search(self, value):
        current_node = self.root
        while(current_node.check_leaf == False):
            temp2 = current_node.values
            for i in range(len(temp2)):
                if (value == temp2[i]):
                    current_node = current_node.keys[i + 1]
                    break
                elif (value < temp2[i]):
                    current_node = current_node.keys[i]
                    break
                elif (i + 1 == len(current_node.values)):
                    current_node = current_node.keys[i + 1]
                    break
        return current_node

    # 查找节点
    def find(self, value, key):
        l = self.search(value)
        for i, item in enumerate(l.values):
            if item == value:
                if key in l.keys[i]:
                    return True
                else:
                    return False
        return False

    # 在父级插入
    def insert_in_parent(self, n, value, ndash):
        if (self.root == n):
            rootNode = Node(n.order)
            rootNode.values = [value]
            rootNode.keys = [n, ndash]
            self.root = rootNode
            n.parent = rootNode
            ndash.parent = rootNode
            return

        parentNode = n.parent
        temp3 = parentNode.keys
        for i in range(len(temp3)):
            if (temp3[i] == n):
                parentNode.values = parentNode.values[:i] + \
                    [value] + parentNode.values[i:]
                parentNode.keys = parentNode.keys[:i +
                                                  1] + [ndash] + parentNode.keys[i + 1:]
                if (len(parentNode.keys) > parentNode.order):
                    parentdash = Node(parentNode.order)
                    parentdash.parent = parentNode.parent
                    mid = int(math.ceil(parentNode.order / 2)) - 1
                    parentdash.values = parentNode.values[mid + 1:]
                    parentdash.keys = parentNode.keys[mid + 1:]
                    value_ = parentNode.values[mid]
                    if (mid == 0):
                        parentNode.values = parentNode.values[:mid + 1]
                    else:
                        parentNode.values = parentNode.values[:mid]
                    parentNode.keys = parentNode.keys[:mid + 1]
                    for j in parentNode.keys:
                        j.parent = parentNode
                    for j in parentdash.keys:
                        j.parent = parentdash
                    self.insert_in_parent(parentNode, value_, parentdash)

    # 删除节点
    def delete(self, value, key):
        node_ = self.search(value)

        temp = 0
        for i, item in enumerate(node_.values):
            if item == value:
                temp = 1

                if key in node_.keys[i]:
                    if len(node_.keys[i]) > 1:
                        node_.keys[i].pop(node_.keys[i].index(key))
                    elif node_ == self.root:
                        node_.values.pop(i)
                        node_.keys.pop(i)
                    else:
                        node_.keys[i].pop(node_.keys[i].index(key))
                        del node_.keys[i]
                        node_.values.pop(node_.values.index(value))
                        self.deleteEntry(node_, value, key)
                else:
                    print("Value not in Key")
                    return
        if temp == 0:
            print("Value not in Tree")
            return

    # 删除条目
    def deleteEntry(self, node_, value, key):

        if not node_.check_leaf:
            for i, item in enumerate(node_.keys):
                if item == key:
                    node_.keys.pop(i)
                    break
            for i, item in enumerate(node_.values):
                if item == value:
                    node_.values.pop(i)
                    break

        if self.root == node_ and len(node_.keys) == 1:
            self.root = node_.keys[0]
            node_.keys[0].parent = None
            del node_
            return
        elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):

            is_predecessor = 0
            parentNode = node_.parent
            PrevNode = -1
            NextNode = -1
            PrevK = -1
            PostK = -1
            for i, item in enumerate(parentNode.keys):

                if item == node_:
                    if i > 0:
                        PrevNode = parentNode.keys[i - 1]
                        PrevK = parentNode.values[i - 1]

                    if i < len(parentNode.keys) - 1:
                        NextNode = parentNode.keys[i + 1]
                        PostK = parentNode.values[i]

            if PrevNode == -1:
                ndash = NextNode
                value_ = PostK
            elif NextNode == -1:
                is_predecessor = 1
                ndash = PrevNode
                value_ = PrevK
            else:
                if len(node_.values) + len(NextNode.values) < node_.order:
                    ndash = NextNode
                    value_ = PostK
                else:
                    is_predecessor = 1
                    ndash = PrevNode
                    value_ = PrevK

            if len(node_.values) + len(ndash.values) < node_.order:
                if is_predecessor == 0:
                    node_, ndash = ndash, node_
                ndash.keys += node_.keys
                if not node_.check_leaf:
                    ndash.values.append(value_)
                else:
                    ndash.nextKey = node_.nextKey
                ndash.values += node_.values

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash

                self.deleteEntry(node_.parent, value_, node_)
                del node_
            else:
                if is_predecessor == 1:
                    if not node_.check_leaf:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm_1 = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [value_] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                p.values[i] = ndashkm_1
                                break
                    else:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [ndashkm] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(p.values):
                            if item == value_:
                                parentNode.values[i] = ndashkm
                                break
                else:
                    if not node_.check_leaf:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [value_]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndashk0
                                break
                    else:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [ndashk0]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndash.values[0]
                                break

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash
                if not node_.check_leaf:
                    for j in node_.keys:
                        j.parent = node_
                if not parentNode.check_leaf:
                    for j in parentNode.keys:
                        j.parent = parentNode


# 输出B+树
def printTree(tree):
    lst = [tree.root]
    level = [0]
    leaf = None
    flag = 0
    lev_leaf = 0

    node1 = Node(str(level[0]) + str(tree.root.values))

    while (len(lst) != 0):
        x = lst.pop(0)
        lev = level.pop(0)
        if (x.check_leaf == False):
            for i, item in enumerate(x.keys):
                print(item.values)
        else:
            for i, item in enumerate(x.keys):
                print(item.values)
            if (flag == 0):
                lev_leaf = lev
                leaf = x
                flag = 1

record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert(&#x27;5&#x27;, &#x27;33&#x27;)
bplustree.insert(&#x27;15&#x27;, &#x27;21&#x27;)
bplustree.insert(&#x27;25&#x27;, &#x27;31&#x27;)
bplustree.insert(&#x27;35&#x27;, &#x27;41&#x27;)
bplustree.insert(&#x27;45&#x27;, &#x27;10&#x27;)

printTree(bplustree)

if(bplustree.find(&#x27;5&#x27;, &#x27;34&#x27;)):
    print("Found")
else:
    print("Not found")

The above is the detailed content of Use Python to write the deletion operation code of B+ tree. For more information, please follow other related articles on the PHP Chinese website!