A query that evaluates a given equation over a range

Evaluating all equations within the interval [L, R] gives us a range of values for these variables. Examples of how to use it include modeling, data analysis, and problem-solving scenarios.
In this case, we define equation variable values for all points within the range. So this can be done by specifying the step size of the range and evaluating the equation for each variable value in the range.
Specification
This can be called a request to the database for information. When certain requirements are met, data is extracted using specific commands. To obtain, filter, sort, and summarize data from a database, queries are often written in programming languages. Queries can be as simple as possible, depending on the complexity of the data and information that must be extracted.
A computer program that accepts as input an equation range [L, R] and a step size and produces the result of the equation for each value of the variable within the range can be used to automate this process.
Problem handling methods
Finding the value of a given equation within a range is the goal of a query that evaluates any given equation in the range [L, R]. Here is a potential approach for a query like -
Parses the provided equation and creates an expression tree from it. Binary trees can be used to visualize expression trees, with each node representing an operator or operand in an equation.
Presort the expression tree and iterate over each subtree, evaluating the equation for each subtree. Each node of the expression tree should contain a result.
Create a range query function that accepts the root of the expression tree, the lower bound L, and the upper bound R as input. The goal of this function is to iterate the expression tree and return the solution to the equation in the provided range [L, R].
The equation solution for each subrange of the specified range [L,R] can be additionally precomputed and saved to improve the range query function.
Finally, we can use the range query function to calculate equations in different ranges.
grammar
In C, you can use a loop to iterate over the values in each range and then apply the provided equation to each value to determine its evaluation within the range [L, R]. Create the following loop to evaluate the equation for each value of x in the range [L, R] -
y = x2 + 2x + 1
// Define equation to evaluate
int equation(int x) {
return x*x + 2*x + 1;
}
// Evaluate equation for every value of x in range [L, R]
int L, R; // Define the range
for (int x = L; x <= R; x++) {
int y = equation(x);
// Do something with value of y like print it
cout << "x = " << x << ", y = " << y << endl;
}
algorithm
This is the C algorithm for evaluating equations in the interval [L, R] -
Step 1 - Give an example of how to define an equation as a function that takes a variable x and returns a value y -
Step 2 - Write a function that accepts two integers L and R as arguments and outputs the solution to the equation for each integer value between L and R. You can use a loop to iterate over the range [L, R], evaluating the equation for each integer value -
Step 3 - After evaluating the equation on the range [L, R], you can use this function to obtain the result, which is passed as a vector of double values -
< /里>vector<double> results = evaluate_equation(1, 10);
Copy after login
double equation(double x) {
return x*x + 2*x + 1;
}
vector<double> evaluate_equation(int L, int R) {
vector<double> results;
for (int x = L; x <= R; x++) {
double y = equation(x);
results.push_back(y);
}
return results;
}
NOTE - You can change the process of calculating any equation by simply replacing the equation function with the desired equation.
Method to follow
method 1
In C, you can evaluate equations in the range [L, R] using a loop that loops over each value in the range and evaluates the equation within it.
The range evaluated in the example is [1, 10], and the equation evaluated is i*i 2*i 1. The for loop repeatedly evaluates the equation for each value in the range and prints the answer to the console. Equations and ranges can be changed as needed.
Example 1
#include <iostream>
using namespace std;
int main() {
int L = 1, R = 10; // range of values to evaluate
for (int i = L; i <= R; i++) {
int result = i*i + 2*i + 1; // equation to evaluate
cout << "Result at " << i << " = " << result << endl;
}
return 0;
}
Output
Result at 1 = 4 Result at 2 = 9 Result at 3 = 16 Result at 4 = 25 Result at 5 = 36 Result at 6 = 49 Result at 7 = 64 Result at 8 = 81 Result at 9 = 100 Result at 10 = 121
Method 2
Here is a description of a C query that can be used to analyze the range of values between L and R for a given equation -
In this diagram, the equation that needs to be calculated is first defined as a function called an equation. We then create an evaluation function that accepts two parameters, L and R, which represent the range of values over which we want to evaluate the equation.
We iteratively evaluate the equation for each value between L and R (inclusive) within the evaluation function. Then, using cout, we print the results for each value.
We specify in the main function the range over which the equation is to be calculated (in this case, L = 1 and R = 10) and call the evaluation function with these values. The programmer's output will be the solution to the problem for each number between 1 and 10.
Example 2
#include <bits/stdc++.h>
using namespace std;
// Define the equation you want to evaluate
int equation(int x) {
return x * x + 2 * x + 1;
}
// Define a function to evaluate the equation for a given range [L, R]
void evaluate(int L, int R) {
for (int i = L; i <= R; i++) {
int result = equation(i);
cout << "The result of equation for " << i << " is " << result << endl;
}
}
int main() {
int L = 1, R = 10;
evaluate(L, R);
return 0;
}
Output
The result of equation for 1 is 4 The result of equation for 2 is 9 The result of equation for 3 is 16 The result of equation for 4 is 25 The result of equation for 5 is 36 The result of equation for 6 is 49 The result of equation for 7 is 64 The result of equation for 8 is 81 The result of equation for 9 is 100 The result of equation for 10 is 121
in conclusion
In summary, we can apply the prefix sum or cumulative sum method to evaluate a given equation within the interval [L,R]. By precomputing the prefix sum of equation values up to each index, each query can be answered in constant time. The time complexity of this strategy (where N is the size of the input array) is O(N) for precomputation and O(1) for each query.
In general, the size of the input array and the number of queries to be run determine which method should be used. If the number of queries is much larger than the size of the array, the prefix sum technique is more efficient. However, if the number of queries is small, a binary search strategy may be a better choice.
The above is the detailed content of A query that evaluates a given equation over a range. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1664
1664
 14
14
 1421
1421
 52
52
 1315
1315
 25
25
 1266
1266
 29
29
 1239
1239
 24
24
 Use java's StringBuilder.replace() function to replace a specified range of characters
Jul 24, 2023 pm 06:12 PM
Use java's StringBuilder.replace() function to replace a specified range of characters
Jul 24, 2023 pm 06:12 PM
Use java's StringBuilder.replace() function to replace a specified range of characters. In Java, the StringBuilder class provides the replace() method, which can be used to replace a specified range of characters in a string. The syntax of this method is as follows: publicStringBuilderreplace(intstart,intend,Stringstr) The above method is used to replace the index star from
 Find numbers that are not divisible by any number in a range, using C++
Sep 13, 2023 pm 09:21 PM
Find numbers that are not divisible by any number in a range, using C++
Sep 13, 2023 pm 09:21 PM
In this article, we will discuss the problem of finding numbers between 1 and n (given) that are not divisible by any number between 2 and 10. Let us understand this with some examples - Input:num=14Output:3Explanation:Therearethreenumbers,1,11,and13,whicharenotdivisible.Input:num=21Output:5Explanation:Therearefivenumbers1,11,13,17,and19,whicharenotdivisible. Solved Simple method if
 How to implement date range selector in Vue?
Jun 25, 2023 am 08:41 AM
How to implement date range selector in Vue?
Jun 25, 2023 am 08:41 AM
How to implement date range selector in Vue? The date range picker is an interface component often used in modern web applications. It allows the user to select a date or a time period from a date range. For web application development that requires a date range selector, Vue.js is a very good choice. Vue.js is a progressive JavaScript framework for building user interfaces. It allows developers to build complex interactive interfaces using componentization.
![[Python NLTK] Text classification, easily solve text classification problems](https://img.php.cn/upload/article/000/465/014/170882739298555.jpg?x-oss-process=image/resize,m_fill,h_207,w_330) [Python NLTK] Text classification, easily solve text classification problems
Feb 25, 2024 am 10:16 AM
[Python NLTK] Text classification, easily solve text classification problems
Feb 25, 2024 am 10:16 AM
Text classification is one of the natural language processing (NLP) tasks that aims to classify text into predefined categories. Text classification has many practical applications, such as email filtering, spam detection, sentiment analysis, and question answering systems, etc. The task of using the pythonNLTK library to complete text classification can be divided into the following steps: Data preprocessing: First, the data needs to be preprocessed, including removing punctuation marks, converting to lowercase, removing spaces, etc. Feature extraction: Next, features need to be extracted from the preprocessed text. Features can be words, phrases, or sentences. Model training: Then, the extracted features need to be used to train a classification model. Commonly used classification models include Naive Bayes, Support Vector Machines, and Decision Trees. Assessment: Final
 Evaluating iqooneo8 and iqooneo9: Which one is more suitable?
Mar 25, 2024 am 09:00 AM
Evaluating iqooneo8 and iqooneo9: Which one is more suitable?
Mar 25, 2024 am 09:00 AM
In the modern society of the 21st century, electronic products have become an indispensable part of people's lives. In this era, e-cigarettes have gradually become a popular consumer product. Among many e-cigarette brands, the two products iqooneo8 and iqooneo9 have attracted much attention. Consumers often hesitate between the two, which one is more suitable? This article will evaluate these two products to help readers make a better choice. First of all, from the perspective of brand background, both iqooneo8 and iqooneo9 belong to the IQOS brand flag.
 How to assess and reduce the risks of MySQL to DB2 technology transformation?
Sep 08, 2023 pm 04:10 PM
How to assess and reduce the risks of MySQL to DB2 technology transformation?
Sep 08, 2023 pm 04:10 PM
How to assess and reduce the risks of MySQL to DB2 technology transformation? Overview: As enterprise business develops and needs change, there may be a need to migrate the MySQL database to a DB2 database. However, database migration inherently carries certain risks, especially when different database technologies are involved. This article will explore how to assess and reduce the risks of MySQL to DB2 technology transformation, and provide some code examples to help readers better understand this process. 1. Risk assessment: Technical transformation from MySQL to DB2
 How to evaluate the applicability of Java functions in different scenarios?
Apr 19, 2024 pm 10:21 PM
How to evaluate the applicability of Java functions in different scenarios?
Apr 19, 2024 pm 10:21 PM
When evaluating the applicability of Java functions, you need to consider function type, input and output, performance, and ease of use. When verifying the validity of an email, the pure function isValidEmail() meets the needs; when looking for the maximum value in a list, the miscellaneous function findMax() is suitable, but you need to pay attention when modifying the input; when concatenating strings, the pure function concatStrings() is convenient and efficient.
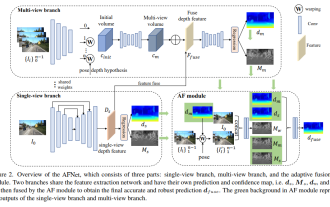 Depth estimation SOTA! Adaptive fusion of monocular and surround depth for autonomous driving
Mar 23, 2024 pm 01:06 PM
Depth estimation SOTA! Adaptive fusion of monocular and surround depth for autonomous driving
Mar 23, 2024 pm 01:06 PM
Written earlier & personally understood that multi-view depth estimation has achieved high performance in various benchmark tests. However, almost all current multi-view systems rely on a given ideal camera pose, which is unavailable in many real-world scenarios, such as autonomous driving. This work proposes a new robustness benchmark to evaluate depth estimation systems under various noisy pose settings. Surprisingly, it is found that current multi-view depth estimation methods or single-view and multi-view fusion methods fail when given noisy pose settings. To address this challenge, here we propose AFNet, a single-view and multi-view fused depth estimation system that adaptively integrates high-confidence multi-view and single-view results to achieve robust and accurate depth estimation. since




