Given an acyclic graph, compute the minimum sum of elements at each depth

A graph that does not contain any cycles or loops is called an acyclic graph. A tree is an acyclic graph in which every node is connected to another unique node. Acyclic graphs are also called acyclic graphs.

The difference between cyclic graphs and acyclic graphs -

The Chinese translation of is:

Cycle Graph	Cycle Graph	Acyclic graph
The graph forms a closed loop.	The chart does not form a closed loop.
Deep loops are not included in the chart	Chart contains every depth.

Example 1

Let’s take an example of a cyclic graph −

When a closed loop exists, a cyclic graph is formed.

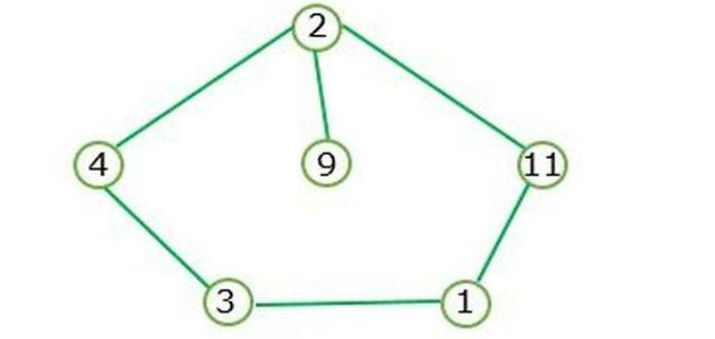
Figure I represents a cycle graph and does not contain depth nodes.

Example 2

is translated as:

Example 2

Let us illustrate with an example of an acyclic graph:

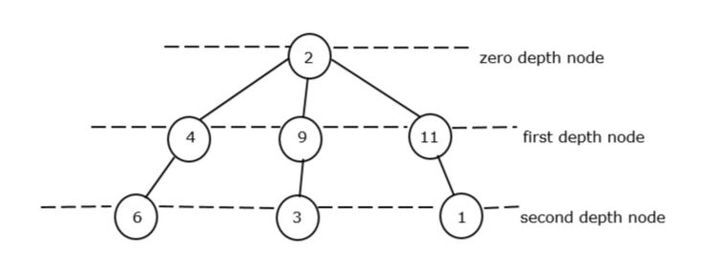
The root node of the tree is called the zero-depth node. In Figure II, there is only one root at zero depth, which is 2. Therefore it is considered a node with a minimum depth of zero.

In the first depth node, we have 3 node elements like 4, 9 and 1, but the smallest element is 4.

In the second depth node we again have 3 node elements like 6, 3 and 1 but the smallest element is 1.

We will know how the total depth node is derived,

Total depth node = Minimum value of Zero_Depth node Minimum value of First_Depth node Minimum value of Zero_Depth node

Total depth nodes = 2 4 3 = 9. So, 9 is the total minimum sum of the acyclic graph.

grammar

The following syntax used in the program:
struct name_of_structure{
   data_type var_name;   
   // data member or field of the structure.
}

• struct − This keyword is used to represent the structure data type.

• name_of_struct - We provide any name for the structure.

• A structure is a collection of various related variables in one place.

Queue < pair < datatype, datatype> > queue_of_pair

make_pair() 

parameter

Pair queue in C -

• This is a generic STL template for combining queue pairs of two different data types, the queue pairs are located under the utility header file.

• Queue_of_pair - We give the pair any name.

• make_pair() - Used to construct a pair object with two elements.

name_of_queue.push()

parameter

• name_of_queue - We are naming the queue name.

• push() − This is a predefined method that is part of the head of the queue. The push method is used to insert elements or values.

name_of_queue.pop()

parameter

• name_of_queue − We are giving the queue a name.

• pop() − This is a predefined method that belongs to the queue header file, and the pop method is used to delete the entire element or value.

algorithm

• We will start the program header files, namely 'iostream', 'climits', 'utility', and 'queue'.

  < /里>

• We are creating a structure "tree_node" with an integer value "val" to get the node value. We then create tree_node pointers with the given data to initialize the left child node and right child node to store the values. Next, we create a tree_node function passing int x as argument and verify that it is equal to the 'val' integer and assign the left and right child nodes as null .

• Now we will define a function minimum_sum_at_each_depth() which accepts an integer value as a parameter to find the minimum sum at each depth. Using an if- statement, it checks if the root value of the tree is empty and returns 0 if it is empty.

• We are creating a queue pair of STL (Standard Template Library) to combine two values.

• We create a queue variable named q that performs two methods as a pair, namely push() and make_pair(). Using these two methods, we insert values ​​and construct two pairs of an object.

• We are initializing three variables namely 'present_depth', 'present_sum' and 'totalSum' which will be used further to find the current sum as well as to find the total minimum sum.

• After initializing the variables, we create a while loop to check the condition, if the queue pair is not empty, the count of the nodes will start from the beginning. Next, we use the 'pop()' method to remove an existing node as it will be moved to the next depth of the tree to calculate the minimum sum.

• Now we will create three if statements to return the minimum sum of the sums.

• After this, we will start the main function and build the tree structure of the input mode with the help of the root pointer, left and right child nodes, and pass the node value through the new 'tree_node' .

• Finally, we call the 'minimum_sum_at_each_depth(root)' function and pass the parameter root to calculate the minimum sum at each depth. Next, print the statement "sum of each depth of the acyclic graph" and get the result.

Remember that a pair queue is a container containing pairs of queue elements.

The Chinese translation of

Example

is:

Example

In this program we will calculate the sum of all minimum nodes for each depth.

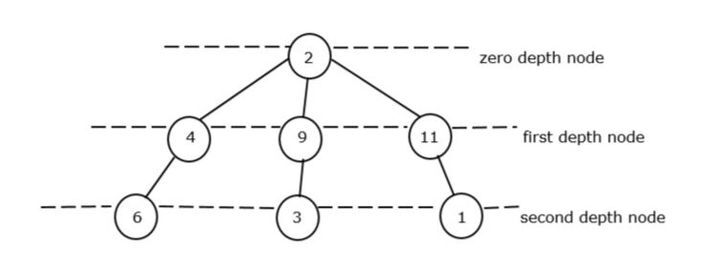
In Figure 2, the minimum sum of the total depth is 15 8 4 1 = 13.

现在我们将把这个数字作为该程序的输入。

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

输出

Total sum at each depth of non cycle graph: 28

结论

我们探讨了给定非循环图中每个深度的元素最小和的概念。我们看到箭头运算符连接节点并构建树形结构，利用它计算每个深度的最小和。该应用程序使用非循环图，例如城市规划、网络拓扑、谷歌地图等。

The above is the detailed content of Given an acyclic graph, compute the minimum sum of elements at each depth. For more information, please follow other related articles on the PHP Chinese website!