Briefly understand the basic ideas and implementation of dichotomy in Java
This article brings you relevant knowledge about java. The dichotomy method is a very efficient algorithm, which is often used in the computer search process. The following will explain the basic idea and implementation of the dichotomy in detail through examples. I hope it will be helpful to everyone.

Recommended study: "java video tutorial"
In an ordered array, find whether a certain number exists

Idea:
- Since it is an ordered array, you can first get the midpoint position, and the midpoint can divide the array into left and right halves.
- If the value of the midpoint position is equal to the target value, return the midpoint position directly.
- If the value of the midpoint position is less than the target value, go to the left side of the midpoint of the array and search in the same way.
- If the value of the midpoint position is greater than the target value, take the right side of the midpoint of the array and search in the same way.
- If it is not found at the end, return: -1.
Code
class Solution {
public int search(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
return m;
} else if (arr[m] > t) {
r = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
}Time complexity O(logN).
In an ordered array, find the leftmost position that is greater than or equal to a certain number
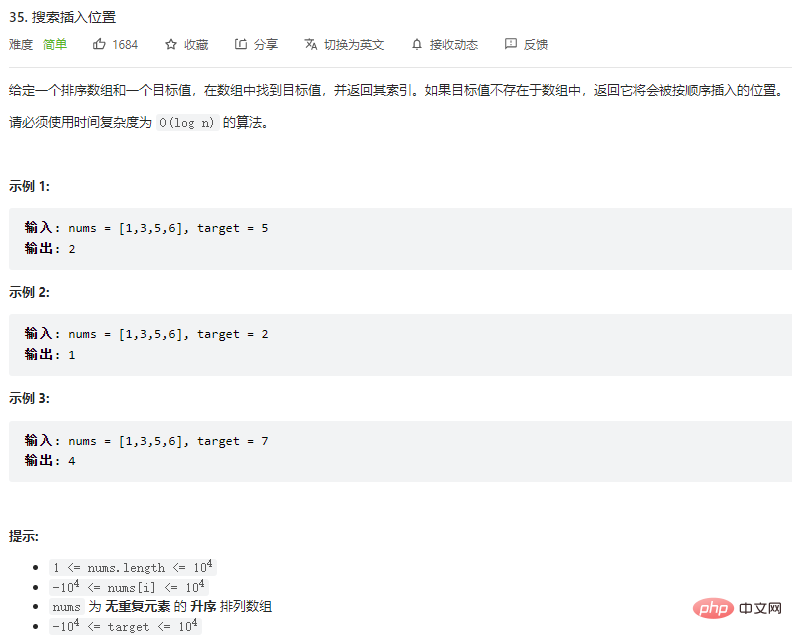
Example 1:
Input: nums = [1,3,5,6], target = 5
Output: 2
Explanation: If you want to insert the element 5 into the array num, It should be inserted between element 3 and element 5, that is, position 2.
Example 2:
Input: nums = [1,3,5,6], target = 2
Output: 1
Explanation: If To insert element 2 into the array num, it should be inserted at the position between element 1 and element 3, that is, position 1.
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Explanation: If To insert the element 7 into the array num, it should be inserted at the end of the array, that is, at position 4.
As you can know from the above example, this question is essentially askingIn an ordered array, find the leftmost position that is greater than or equal to a certain number. If it does not exist, return the length of the array (representing Insert at the end position)
We only need to make simple changes based on the above example. In the above example, if we find the position that meets the conditions, we can directly return
if (arr[m] == t) {
return m;
}In this question, because we need to find the leftmost position, when encounters equality, we only need to record the position first, without returning directly, and then continue to search on the left Is there any position further to the left that meets the conditions?
At the same time, when encountering arr[m] > t, you also need to record the m position at this time, because this may also is a location that satisfies the conditions.
Code:
class Solution {
public static int searchInsert(int[] arr, int t) {
int ans = arr.length;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l)>>1);
if (arr[m] >= t) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
}The time complexity of the entire algorithm is O(logN).
Find the first and last position of the element in the sorted array
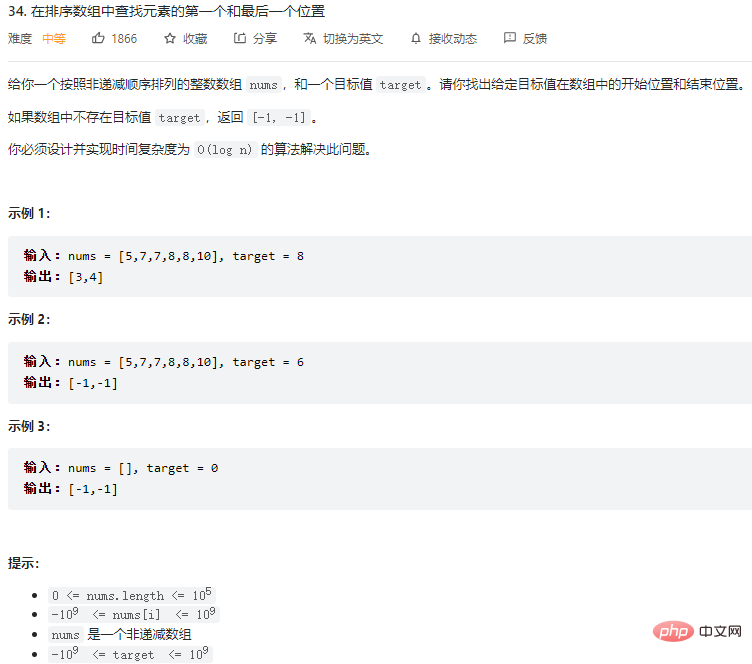
Ideas
This question is also solved using binary division. When an element is found through binary division, do not rush back, but continue to search to the left (right) to see if you can find a matching value further to the left (right).
The code is as follows:
class Solution {
public static int[] searchRange(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return new int[]{-1, -1};
}
return new int[]{left(arr,t),right(arr,t)};
}
public static int left(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
r = m - 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
public static int right(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
l = m + 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
}Time complexity O(logN).
Local maximum problem

Idea
Assume that the length of the array is N, first determine 0 Are the number at position and the number at position N-1 the peak position? The
0 position only needs to be compared with the 1 position. If the 0 position is larger, the 0 position It is the peak position and can be returned directly. The
N-1 position only needs to be compared with the N-2 position. If the N-1 position is larger, Position N-1 is the peak position and can be returned directly.
If the 0 position and N-1 are both minimum values in the last round of comparison, then the array must look like the following:

As can be seen from the above figure, the [0..1] interval is a growth trend, [N-2...N-1] Within the range is a downward trend.
Then the peak position must appear between [1...N-2].
At this time, you can find the peak position by bisection, first go to the midpoint position, assuming it is mid, if the value of the midpoint position is greater than the value of the left and right sides Duda:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
then the mid position is the peak position and returns directly.
Otherwise, there are two situations as follows:
Case 1: The value of mid position is smaller than the value of mid - 1 position
趋势如下图:

则在[1...(mid-1)]区间内继续二分。
情况二:mid 位置的值比 mid + 1 位置的值小
趋势是:

则在[(mid+1)...(N-2)]区间内继续上述二分。
完整代码
public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}时间复杂度O(logN)。
推荐学习:《java视频教程》
The above is the detailed content of Briefly understand the basic ideas and implementation of dichotomy in Java. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1657
1657
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1230
1230
 24
24
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 PHP: A Key Language for Web Development
Apr 13, 2025 am 12:08 AM
PHP: A Key Language for Web Development
Apr 13, 2025 am 12:08 AM
PHP is a scripting language widely used on the server side, especially suitable for web development. 1.PHP can embed HTML, process HTTP requests and responses, and supports a variety of databases. 2.PHP is used to generate dynamic web content, process form data, access databases, etc., with strong community support and open source resources. 3. PHP is an interpreted language, and the execution process includes lexical analysis, grammatical analysis, compilation and execution. 4.PHP can be combined with MySQL for advanced applications such as user registration systems. 5. When debugging PHP, you can use functions such as error_reporting() and var_dump(). 6. Optimize PHP code to use caching mechanisms, optimize database queries and use built-in functions. 7
 PHP vs. Python: Understanding the Differences
Apr 11, 2025 am 12:15 AM
PHP vs. Python: Understanding the Differences
Apr 11, 2025 am 12:15 AM
PHP and Python each have their own advantages, and the choice should be based on project requirements. 1.PHP is suitable for web development, with simple syntax and high execution efficiency. 2. Python is suitable for data science and machine learning, with concise syntax and rich libraries.
 PHP vs. Other Languages: A Comparison
Apr 13, 2025 am 12:19 AM
PHP vs. Other Languages: A Comparison
Apr 13, 2025 am 12:19 AM
PHP is suitable for web development, especially in rapid development and processing dynamic content, but is not good at data science and enterprise-level applications. Compared with Python, PHP has more advantages in web development, but is not as good as Python in the field of data science; compared with Java, PHP performs worse in enterprise-level applications, but is more flexible in web development; compared with JavaScript, PHP is more concise in back-end development, but is not as good as JavaScript in front-end development.
 PHP vs. Python: Core Features and Functionality
Apr 13, 2025 am 12:16 AM
PHP vs. Python: Core Features and Functionality
Apr 13, 2025 am 12:16 AM
PHP and Python each have their own advantages and are suitable for different scenarios. 1.PHP is suitable for web development and provides built-in web servers and rich function libraries. 2. Python is suitable for data science and machine learning, with concise syntax and a powerful standard library. When choosing, it should be decided based on project requirements.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 PHP's Impact: Web Development and Beyond
Apr 18, 2025 am 12:10 AM
PHP's Impact: Web Development and Beyond
Apr 18, 2025 am 12:10 AM
PHPhassignificantlyimpactedwebdevelopmentandextendsbeyondit.1)ItpowersmajorplatformslikeWordPressandexcelsindatabaseinteractions.2)PHP'sadaptabilityallowsittoscaleforlargeapplicationsusingframeworkslikeLaravel.3)Beyondweb,PHPisusedincommand-linescrip
 PHP: The Foundation of Many Websites
Apr 13, 2025 am 12:07 AM
PHP: The Foundation of Many Websites
Apr 13, 2025 am 12:07 AM
The reasons why PHP is the preferred technology stack for many websites include its ease of use, strong community support, and widespread use. 1) Easy to learn and use, suitable for beginners. 2) Have a huge developer community and rich resources. 3) Widely used in WordPress, Drupal and other platforms. 4) Integrate tightly with web servers to simplify development deployment.




