Mean Squared Error: Definition and Formula
Introduction
Mean squared error (MSE), a fundamental concept in statistics and machine learning, is a key metric for assessing model accuracy. It quantifies the discrepancy between a model's predictions and the actual values. MSE's simplicity and effectiveness make it a popular choice for evaluating model performance. This article explores mean squared error through practical examples.
Overview
This article covers:
- The mathematical definition and representation of mean squared error.
- Calculating MSE for a given set of actual and predicted values.
- Understanding MSE's sensitivity to outliers and its implications for model evaluation.
- Comparing MSE with other error metrics, such as Root Mean Squared Error and Mean Absolute Error.
- Applying MSE in real-world scenarios, including forecasting, hyperparameter tuning, and model assessment.
Table of contents
- What is Mean Squared Error?
- Key Concepts
- Examples
- Practical Applications
- Limitations
- Frequently Asked Questions
What is Mean Squared Error?
Mean squared error represents the average of the squared differences between predicted and observed values. Mathematically:

Squaring the errors prevents positive and negative differences from canceling each other out. Furthermore, squaring amplifies the impact of larger errors, making MSE particularly sensitive to outliers.
Key Concepts
Understanding these concepts is crucial for working with MSE:
Error Calculation
The error for each prediction is the difference between the predicted and actual value. This indicates the prediction's accuracy, with positive or negative values representing over- or under-estimation.
Averaging Squared Errors
The mean squared error is calculated by summing the squared errors and dividing by the number of observations. This averaging provides a scaled measure of the average prediction error.
Outlier Sensitivity
MSE's sensitivity to outliers stems from the squaring operation. Large errors are disproportionately weighted, significantly influencing the overall MSE value.
Comparison with Other Metrics
- Mean Absolute Error (MAE): MAE averages the absolute differences, unlike MSE. Less sensitive to outliers, MAE doesn't penalize large errors as severely.
- Root Mean Squared Error (RMSE): RMSE is the square root of MSE. Expressed in the original data's units, RMSE offers better interpretability.
Examples
Let's illustrate MSE calculation with examples:
Example 1: Simple Linear Regression
Consider a simple linear regression model predicting house prices based on size:
| Actual Price ($) | Predicted Price ($) |
|---|---|
| 200,000 | 195,000 |
| 250,000 | 260,000 |
| 300,000 | 310,000 |
| 350,000 | 345,000 |
| 400,000 | 390,000 |
The MSE calculation involves these steps:
1. Calculate errors:

2. Square the errors:

3. Sum the squared errors:

4. Divide by the number of observations:

The resulting MSE is 70,000,000.
Example 2: Model Comparison
Suppose two models predict the same data, with Model A having an MSE of 10,000 and Model B having an MSE of 5,000. Model B is preferred due to its lower MSE, indicating better predictive accuracy.
Practical Applications
MSE finds application in various areas:
Model Evaluation
MSE is frequently used to compare the performance of different regression models. The model with the lowest MSE is generally considered the most accurate.
Hyperparameter Tuning
During model training, MSE can serve as a loss function, guiding the optimization process. Minimizing MSE helps find optimal model parameters.
Forecasting
In time series analysis, MSE assesses the accuracy of forecasts. Lower MSE values signify more precise predictions, crucial for informed decision-making.
Limitations
Despite its usefulness, MSE has limitations:
- Outlier Sensitivity: Large errors disproportionately influence MSE.
- Interpretability: MSE's units are the square of the original data's units, potentially reducing interpretability.
Conclusion
Mean Squared Error is a vital metric for evaluating the accuracy of predictive models. Its simplicity and efficiency make it a popular choice for model comparison and evaluation. However, for a comprehensive analysis, consider using additional metrics like MAE and RMSE, and be mindful of its sensitivity to outliers. Understanding MSE's strengths and limitations leads to better model development and more accurate predictions.
Frequently Asked Questions
Q1. What is MSE? A. Mean Squared Error (MSE) measures the average squared difference between predicted and actual values, assessing a model's predictive accuracy.
Q2. Why is MSE sensitive to outliers? A. The squaring of errors in MSE amplifies the impact of large errors, making it sensitive to outliers.
Q3. When should I use MSE over other error metrics? A. MSE is often used alongside MAE and RMSE. It's particularly useful when large errors are highly undesirable.
The above is the detailed content of Mean Squared Error: Definition and Formula. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1658
1658
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1231
1231
 24
24
 Getting Started With Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
Getting Started With Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
Meta's Llama 3.2: A Leap Forward in Multimodal and Mobile AI Meta recently unveiled Llama 3.2, a significant advancement in AI featuring powerful vision capabilities and lightweight text models optimized for mobile devices. Building on the success o
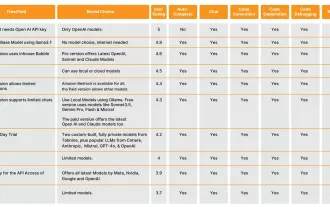 10 Generative AI Coding Extensions in VS Code You Must Explore
Apr 13, 2025 am 01:14 AM
10 Generative AI Coding Extensions in VS Code You Must Explore
Apr 13, 2025 am 01:14 AM
Hey there, Coding ninja! What coding-related tasks do you have planned for the day? Before you dive further into this blog, I want you to think about all your coding-related woes—better list those down. Done? – Let’
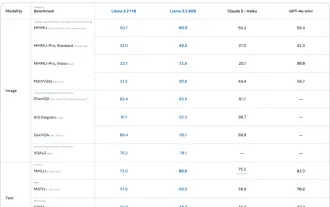 AV Bytes: Meta's Llama 3.2, Google's Gemini 1.5, and More
Apr 11, 2025 pm 12:01 PM
AV Bytes: Meta's Llama 3.2, Google's Gemini 1.5, and More
Apr 11, 2025 pm 12:01 PM
This week's AI landscape: A whirlwind of advancements, ethical considerations, and regulatory debates. Major players like OpenAI, Google, Meta, and Microsoft have unleashed a torrent of updates, from groundbreaking new models to crucial shifts in le
 Selling AI Strategy To Employees: Shopify CEO's Manifesto
Apr 10, 2025 am 11:19 AM
Selling AI Strategy To Employees: Shopify CEO's Manifesto
Apr 10, 2025 am 11:19 AM
Shopify CEO Tobi Lütke's recent memo boldly declares AI proficiency a fundamental expectation for every employee, marking a significant cultural shift within the company. This isn't a fleeting trend; it's a new operational paradigm integrated into p
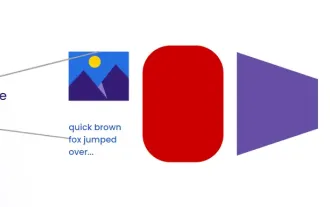 A Comprehensive Guide to Vision Language Models (VLMs)
Apr 12, 2025 am 11:58 AM
A Comprehensive Guide to Vision Language Models (VLMs)
Apr 12, 2025 am 11:58 AM
Introduction Imagine walking through an art gallery, surrounded by vivid paintings and sculptures. Now, what if you could ask each piece a question and get a meaningful answer? You might ask, “What story are you telling?
 GPT-4o vs OpenAI o1: Is the New OpenAI Model Worth the Hype?
Apr 13, 2025 am 10:18 AM
GPT-4o vs OpenAI o1: Is the New OpenAI Model Worth the Hype?
Apr 13, 2025 am 10:18 AM
Introduction OpenAI has released its new model based on the much-anticipated “strawberry” architecture. This innovative model, known as o1, enhances reasoning capabilities, allowing it to think through problems mor
 How to Add a Column in SQL? - Analytics Vidhya
Apr 17, 2025 am 11:43 AM
How to Add a Column in SQL? - Analytics Vidhya
Apr 17, 2025 am 11:43 AM
SQL's ALTER TABLE Statement: Dynamically Adding Columns to Your Database In data management, SQL's adaptability is crucial. Need to adjust your database structure on the fly? The ALTER TABLE statement is your solution. This guide details adding colu
 Newest Annual Compilation Of The Best Prompt Engineering Techniques
Apr 10, 2025 am 11:22 AM
Newest Annual Compilation Of The Best Prompt Engineering Techniques
Apr 10, 2025 am 11:22 AM
For those of you who might be new to my column, I broadly explore the latest advances in AI across the board, including topics such as embodied AI, AI reasoning, high-tech breakthroughs in AI, prompt engineering, training of AI, fielding of AI, AI re




