为什么说浮点数缺乏精确性? python中浮点数运算问题
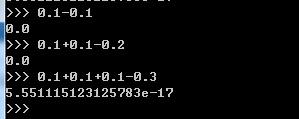 python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教
python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教回复内容:
这是因为小数以二进制形式表示时的有穷性导致的。(下面的说法,不完全准确,只是帮助理解)以下是之前我在另一个地方对一个类似问题的解答,因为内容差不多,就直接搬过来了(本人略懒,希望有所帮助):
#################################此处开始####################################
我们知道,将一个小数转化为二进制表示的方式是,不断的乘2,取其中的整数部分。例如:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.625*2 = 1.25, 整数部分为1,小数部分为0.25
(2) 0.25 * 2 = 0.5 , 整数部分为0,小数部分为0.5
(3) 0.5 * 2 = 1 , 整数部分为1,小数部分为0
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.625的二进制表示就是0.101。
然而有些小数,例如0.4,并不能够精确的转化为二进制表示,用上面的这种方法计算:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.4*2=0.8 整数部分为0,小数部分为0.8
(2) 0.8*2=1.6 整数部分为1,小数部分为0.6
(3) 0.6*2=1.2 整数部分为1,小数部分为0.2
(4) 0.2*2=0.4 整数部分为0,小数部分为0.4
(5) 0.4*2=0.8 整数部分为0,小数部分为0.8
(6) 0.8*2=1.6 整数部分为1,小数部分为0.6
(7) 0.6*2=1.2 整数部分为1,小数部分为0.2
……
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.4转化为二进制,应该是0.0110... 这样一个无限循环小数。
计算机的内存、cpu寄存器等等这些硬件单元都是有限的,只能表示有限位数的二进制位,因此存储的二进制小数就会和实际转换而成的二进制数有一定的误差。(你可以试着将0.3转化为二进制表示,也将出现一个循环小数。)
实际上,大多数情况下,小数在计算机中是以一种类似科学计数法的形式表示的,具体的可以参考一下其他的资料。但即便如此,仍然存在误差。
所以在python中不建议直接将两个浮点数进行大小比较,或者做精确的计算,往往会得到意想不到的结果。当然,如果非要用,可以参考decimal模块的相关内容。 请将十进制数字0.1转换成二进制浮点数。 这不是Python的问题,而是实数的无限精度跟计算机的有限内存之间的矛盾。
举个例子,假如说我只能使用整数(即只精确到个位,计算机内的浮点数也只有有限精度,以C语言中的双精度浮点数double为例,精度为52个二进制位),要表示任意实数(无限精度)的时候我就只能通过舍入(rounding)来近似表示。
比如1.2我会表示成1,2.4表示成2,3.6表示成4.
所以呢?
在算1.2 - 1.2的时候,由于计算机表示的问题,我算的实际上是1 - 1,结果是0,碰巧蒙对了;
在算1.2 + 1.2 - 2.4的时候,由于计算机表示的问题,我算的实际上是1 + 1 - 2,结果是0,再次蒙对了;
但是在算1.2 + 1.2 + 1.2 - 3.6的时候,由于计算机表示的问题,我算的实际上是1 + 1 + 1 - 4,结果是-1,运气没那么好啦!
这里的1.2, 2.4, 3.6就相当于你问题里的0.1, 0.2和0.3,1, 2, 4则是真正在计算机内部进行运算的数值,我说清楚了吗?
其他请看IEEE 754浮点数标准,比如CSAPP第二章啥的(虽然估计你没兴趣看)。
另:不仅仅是浮点数的在计算机内部的表示有误差,运算本身也可能会有误差。比如整数2可以在计算机内准确表示,但是要算根号2就有误差了;再比如两个浮点数相除,本来两个数都是精确表示的,但除的结果精度却超出了计算机内实数的表示范围,然后就有误差了。 计算机智能处理可数集合的运算,但是全体实数是不可数的,所以计算机只能用一些奇怪的方法来拟合他,于是就产生了浮点数。 这个不是python 的问题,所有基于二进制的浮点数都会有这个问题,原因在于大部分浮点数转换为二进制后都是无限循环小数,而浮点数不可能用无限大的内存来储存,所以会有舍入的误差
详细可以看代码之谜(五) 来个 @vczh 答案的通俗版,比如用 10 个箱子装100个球,规定每个箱子只能装一个球,那显然是装不下所有球的。类似,double类型是 64bit 的,最多能表达 2^64 个数,实数有多少呢?无数个,所以 double 类型是装不下所有实数的,只能表达一个近似值。 9.4. decimal 计算机所有信息的存储使用二进制表示,像 @vczh 所说,有限的「位」,无法表示无数个数,那么,小数用二进制表示法,只能表示那些能被写成
 的数。
的数。0.1 的二进制表示为 0.000110011[0011]...,因为是无限循环的,无法用有限的位表示,所以计算机系统会进行舍入,以求用最接近的值来表示,这里涉及到不同的舍入方式,具体请见深入理解计算机系统,本答案也是参考该书。 大白话版的很多人都说了,就是计算机有限的数字表示不了数学中无穷的数。
楼主如果有一定计算机或者数学基础可以搜一下IEEE754,电脑是如何表示浮点数的一种协议。看懂了那个协议就知道为什么了~
如果看不懂IEEE754那就需要研究下数学中各种进制~主要是二进制、十进制和他们的关系。 自傲的人类!有本事你直接喂它2进制数,看看还有没有这种精度问题。

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 PHP和Python:解释了不同的范例
Apr 18, 2025 am 12:26 AM
PHP和Python:解释了不同的范例
Apr 18, 2025 am 12:26 AM
PHP主要是过程式编程,但也支持面向对象编程(OOP);Python支持多种范式,包括OOP、函数式和过程式编程。PHP适合web开发,Python适用于多种应用,如数据分析和机器学习。
 在PHP和Python之间进行选择:指南
Apr 18, 2025 am 12:24 AM
在PHP和Python之间进行选择:指南
Apr 18, 2025 am 12:24 AM
PHP适合网页开发和快速原型开发,Python适用于数据科学和机器学习。1.PHP用于动态网页开发,语法简单,适合快速开发。2.Python语法简洁,适用于多领域,库生态系统强大。
 PHP和Python:深入了解他们的历史
Apr 18, 2025 am 12:25 AM
PHP和Python:深入了解他们的历史
Apr 18, 2025 am 12:25 AM
PHP起源于1994年,由RasmusLerdorf开发,最初用于跟踪网站访问者,逐渐演变为服务器端脚本语言,广泛应用于网页开发。Python由GuidovanRossum于1980年代末开发,1991年首次发布,强调代码可读性和简洁性,适用于科学计算、数据分析等领域。
 Python vs. JavaScript:学习曲线和易用性
Apr 16, 2025 am 12:12 AM
Python vs. JavaScript:学习曲线和易用性
Apr 16, 2025 am 12:12 AM
Python更适合初学者,学习曲线平缓,语法简洁;JavaScript适合前端开发,学习曲线较陡,语法灵活。1.Python语法直观,适用于数据科学和后端开发。2.JavaScript灵活,广泛用于前端和服务器端编程。
 sublime怎么运行代码python
Apr 16, 2025 am 08:48 AM
sublime怎么运行代码python
Apr 16, 2025 am 08:48 AM
在 Sublime Text 中运行 Python 代码,需先安装 Python 插件,再创建 .py 文件并编写代码,最后按 Ctrl B 运行代码,输出会在控制台中显示。
 Golang vs. Python:性能和可伸缩性
Apr 19, 2025 am 12:18 AM
Golang vs. Python:性能和可伸缩性
Apr 19, 2025 am 12:18 AM
Golang在性能和可扩展性方面优于Python。1)Golang的编译型特性和高效并发模型使其在高并发场景下表现出色。2)Python作为解释型语言,执行速度较慢,但通过工具如Cython可优化性能。
 vscode在哪写代码
Apr 15, 2025 pm 09:54 PM
vscode在哪写代码
Apr 15, 2025 pm 09:54 PM
在 Visual Studio Code(VSCode)中编写代码简单易行,只需安装 VSCode、创建项目、选择语言、创建文件、编写代码、保存并运行即可。VSCode 的优点包括跨平台、免费开源、强大功能、扩展丰富,以及轻量快速。
 notepad 怎么运行python
Apr 16, 2025 pm 07:33 PM
notepad 怎么运行python
Apr 16, 2025 pm 07:33 PM
在 Notepad 中运行 Python 代码需要安装 Python 可执行文件和 NppExec 插件。安装 Python 并为其添加 PATH 后,在 NppExec 插件中配置命令为“python”、参数为“{CURRENT_DIRECTORY}{FILE_NAME}”,即可在 Notepad 中通过快捷键“F6”运行 Python 代码。






