迄今，人们对神经网络的一大疑虑是，它是难以解释的黑盒。本文则主要从理论上理解为什么神经网络对模式识别、分类效果这么好，其本质是通过一层层仿射变换和非线性变换把原始输入做扭曲和变形，直至可以非常容易被区分不同的类别。 实际上，反向传播算法（BP) 其实就是根据训练数据不断地微调这个扭曲的效果。
大约十年前开 始， 深 度 神经 网络 在计算 机视觉等领域取得了突破性成果，引起了极大的兴趣和关注。
然而，仍有一些人对此表示忧虑。原因之一是，神经网络是一个黑匣子：如果神经网络训练得很好，可以获得高质量的结果，但很难理解它的工作原理。如果神经网络出现故障，也很难找出问题所在。
虽然要整体理解深层神经网络很难，但可以从低维深层神经网络入手，也就是每层只有几个神经元的网络，它们理解起来要容易得多。我们可以通过可视化方法来理解低维深层神经网络的行为和训练。可视化方法能让我们更直观地了解神经网络的行为，并观察到神经网络和 拓扑 学之间的联系。
接下来我会谈及许多有趣的事情，包括能够对特定数据集进行分类的神经网络的复杂性下限。
让我们从一个非常简单的数据集开始。下图中，平面上的两条曲线由无数的点组成。神经网络将试着区分这些点分别属于哪一条线。
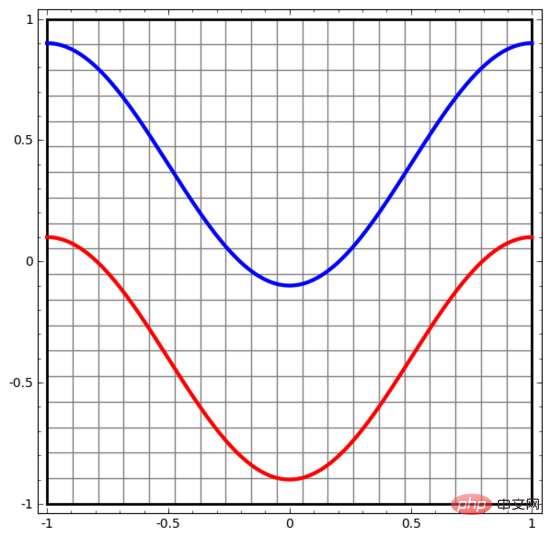
要观察神经网络（或任何分类算法）的行为，最直接的方法就是看看它是如何对每个数据点进行分类的。
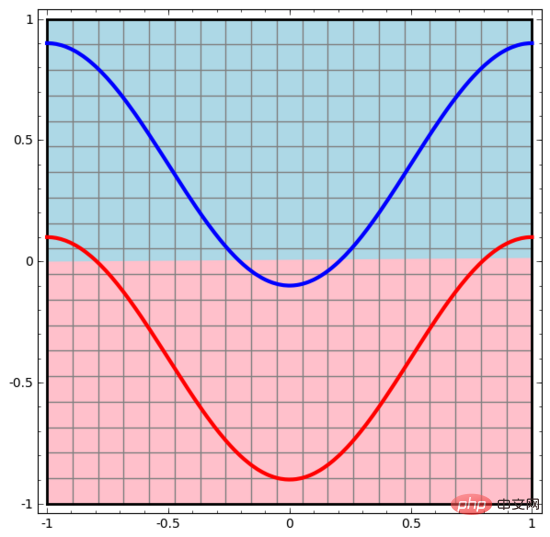
我们从最简单的神经网络开始观察，它只有一个输入层和一个输出层。这样的神经网络只是用一条直线将两类数据点分开。
这样的神经网络太简单粗暴了。现代神经网络通常在输入层和输出层之间有多个层，称为隐藏层。再简单的现代神经网络起码有一个隐藏层。
一个简单的神经网络，图源维基百科
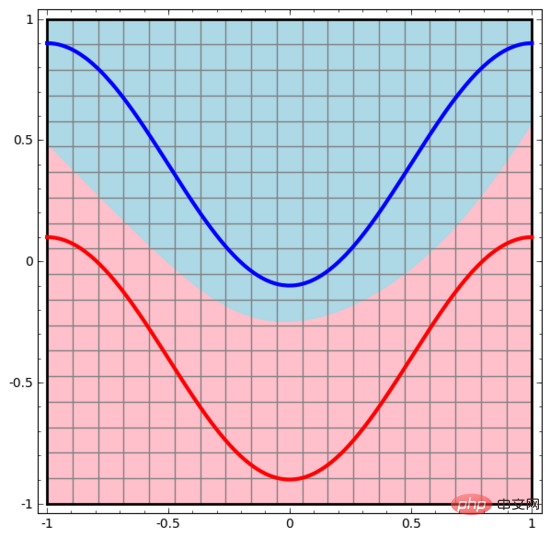
同样地，我们观察神经网络对每个数据点所做的操作。可见，这个神经网络用一条曲线而不是直线来分离数据点。显然，曲线比直线更复杂。
神经网络的每一层都会用一个新的表示形式来表示数据。我们可以观察数据如何转化成新的表示形式以及神经网络如何对它们进行分类。在最后一层的表示形式中，神经网络会在两类数据之间画一条线来区分（如果在更高的维度中，就会画一个超平面）。
在前面的可视化图形中，我们看到了数据的原始表示形式。你可以把它视为数据在「输入层」的样子。现在我们看看数据被转化之后的样子，你可以把它视为数据在「隐藏层」中的样子。
数据的每一个维度都对应神经网络层中一个神经元的激活。
隐藏层用如上方法表示数据，使数据可以被一条直线分离 （即线性可分）
在上一节的方法中，神经网络的每一层用不同表示形式来表示数据。这样一来，每层的表示形式之间是离散的，并不连续。
这就给我们的理解造成困难，从一种表示形式到另一种表示形式，中间是如何转换的呢？好在，神经网络层的特性让这方面的理解变得非常容易。
神经网络中有各种不同的层。下面我们将以tanh层作为具体例子讨论。一个tanh层 ，包括：
我们可以将其视为一个连续的转换，如下所示：
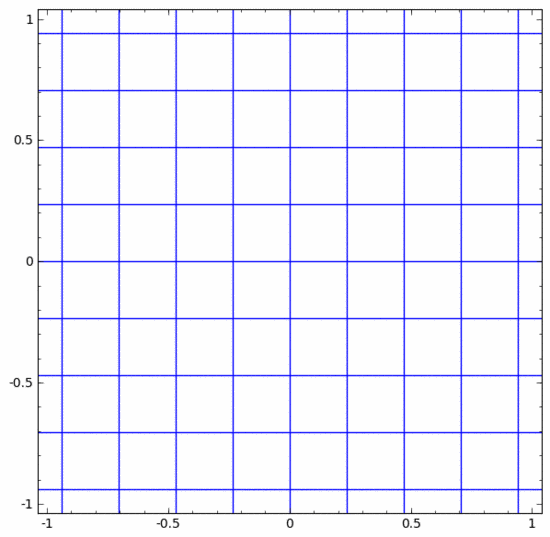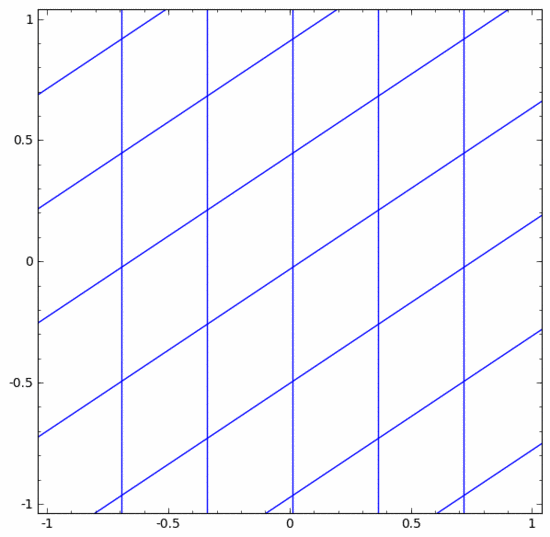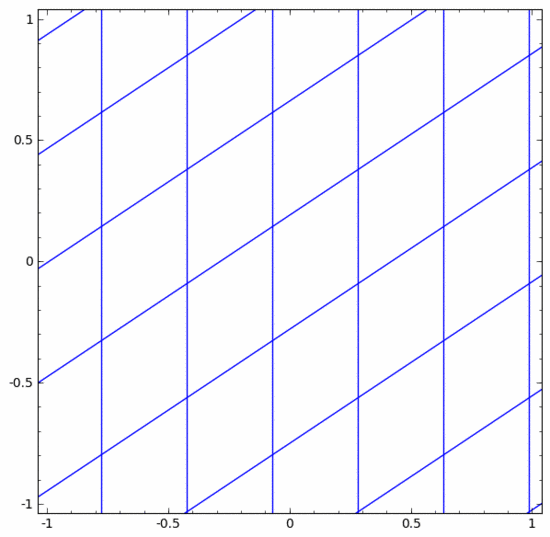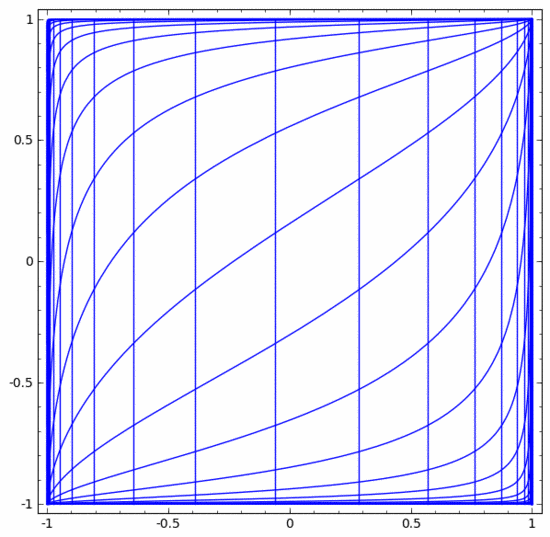
其他标准层的情况大致相同，由仿射变换和单调激活函数的逐点应用组成。
我们可以用这种方法来理解更复杂的神经网络。例如，下面的神经网络使用四个隐藏层对两条略有互缠的螺旋线进行分类。可以看到，为了对数据进行分类，数据的表示方式被不断转换。两条螺旋线最初是纠缠在一起的，但到最后它们可以被一条直线分离（线性可分）。
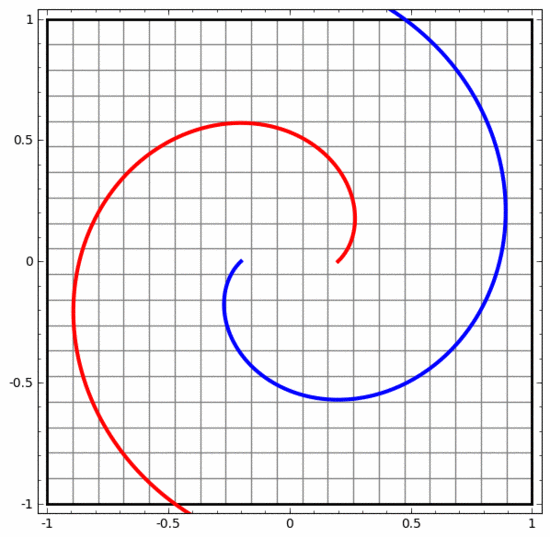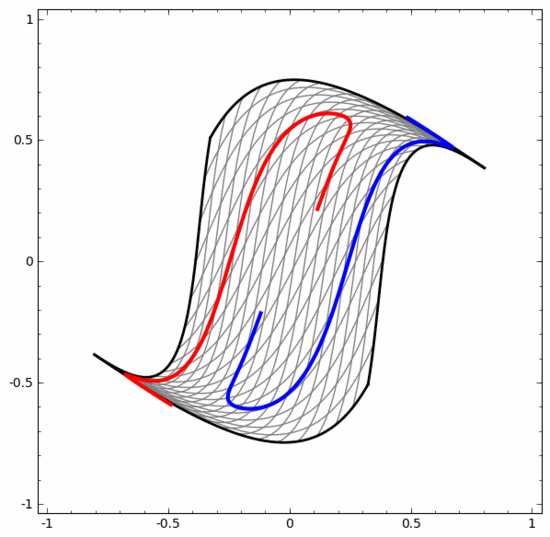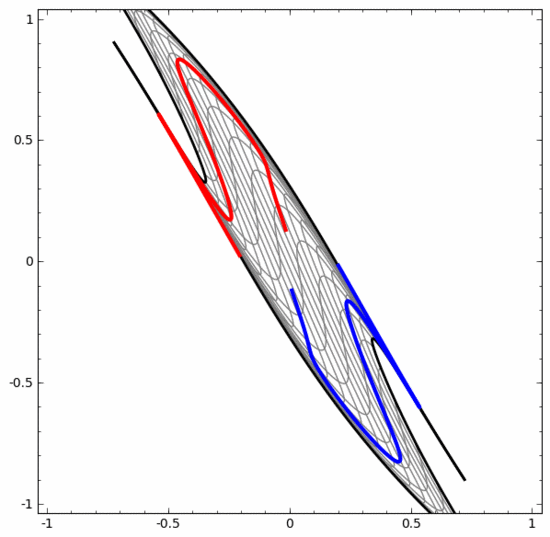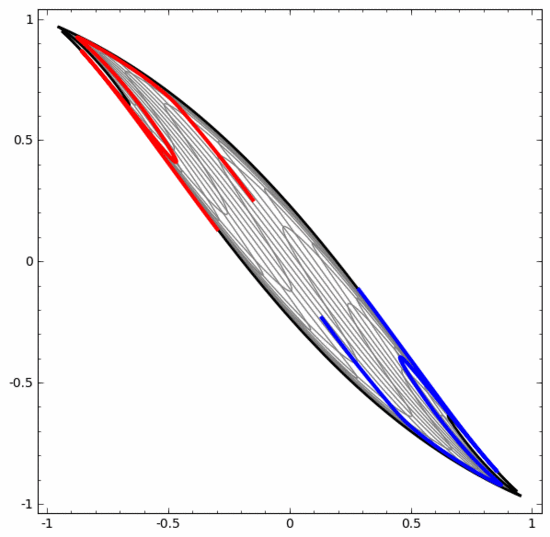
另一方面，下面的神经网络，虽然也使用多个隐藏层，却无法划分两条互缠程度更深的螺旋线。
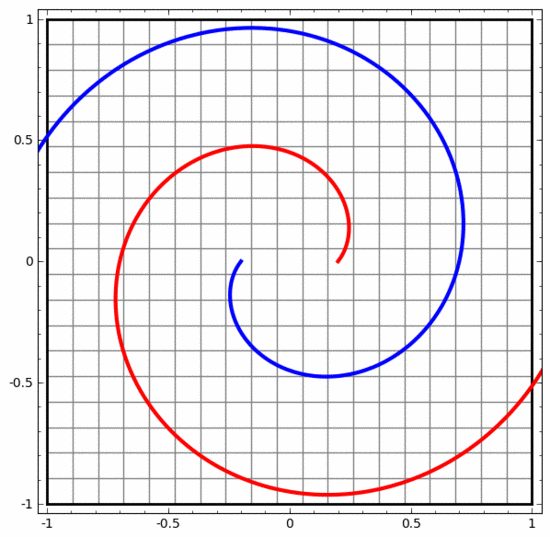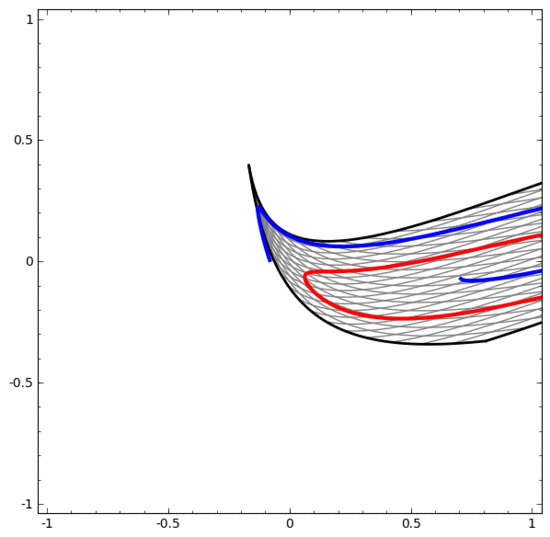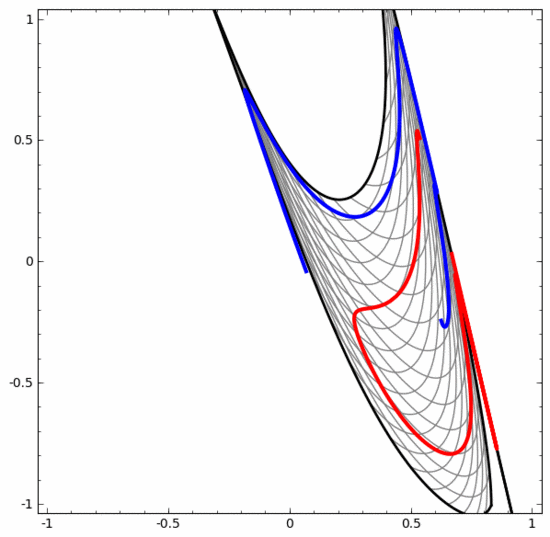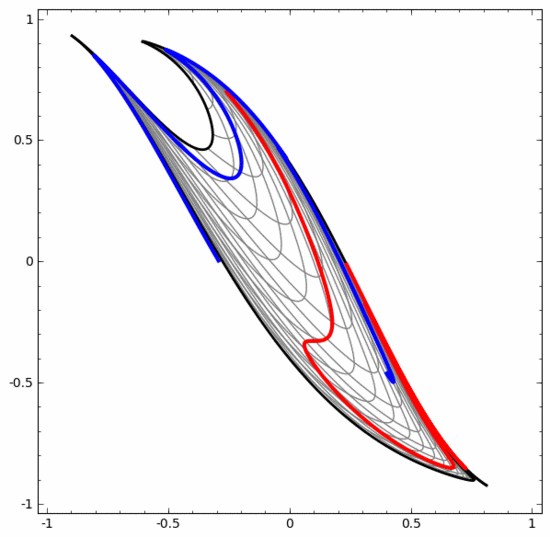
需要明确指出的是，以上两个螺旋线分类任务有一些挑战，因为我们现在使用的只是低维神经网络。如果我们使用宽度更大的神经网络，一切都会很容易很多。
（Andrej Karpathy基于ConvnetJS制作了一个很好的demo，让人可以通过这种可视化的训练交互式地探索神经网络。）
神经网络的每一层都会拉伸和挤压空间，但它不会剪切、割裂或折叠空间。直观上看，神经网络不会破坏数据的拓扑性质。例如，如果一组数据是连续的，那么它被转换表示形式之后也是连续的（反之亦然）。
像这样不影响拓扑性质的变换称为同胚（homeomorphisms）。形式上，它们是双向连续函数的双射。
定理 ：如果权重矩阵 W 是非奇异的（non-singular），而神经网络的一层有N个输入和N个输出，那么这层的映射是同胚（对于特定的定义域和值域而言）。
证明 ：让我们一步一步来：
1. 假设 W 存在非零行列式。那么它是一个具有线性逆的双射线性函数。线性函数是连续的。那么“乘以 W ”这样的变换就是同胚；
2. “平移”变换是同胚；
3. tanh（还有s igmoid和softplus，但不包括ReLU）是具有连续逆（continuous inverses）的 连续函数。（对于特定的定义域和值域而言），它们就是双射，对它们的逐点应用就是同胚。
因此，如果 W 存在一个非零行列式，这一个神经网络层就是同胚。
如果我们将这样的层随意组合在一起，这个结果仍然成立。
4、拓扑与分类
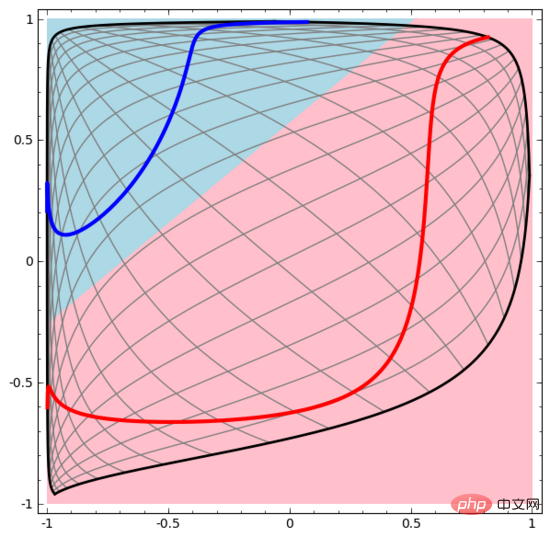
我们来看一个二维数据集，它包含两类数据A和B：
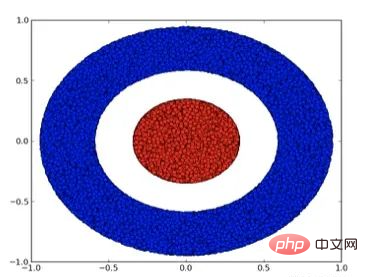
A是红色，B是蓝色
说明 ：要对这个数据集进行分类，神经网络（不管深度如何）必须有一个包含3个或以上隐藏单元的层。
如前所述，使用sigmoid单元或softmax层进行分类，相当于在最后一层的表示形式中找到一个超平面（在本例中则是直线）来分隔 A 和 B。如果只有两个隐藏单元，神经网络在拓扑上就无法以这种方式分离数据，也就无法对上述数据集进行分类。
在下面的可视化中，隐藏层转换对数据的表示形式，直线为分割线。可见，分割线不断旋转、移动，却始终无法很好地分隔A和B两类数据。
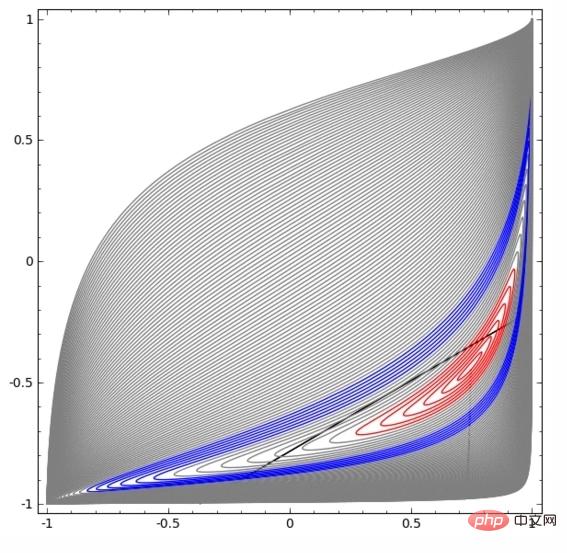
这样的神经网络再怎么训练也无法很好地完成分类任务
最后它只能勉强实现一个局部最小值，达到80%的分类精度。
上述例子只有一个隐藏层，由于只有两个隐藏单元，所以无论如何它都会分类失败。
证明 ：如果只有两个隐藏单元，要么这层的转换是同胚，要么层的权重矩阵有行列式0。如果是同胚的话，A仍然被B包围，不能用一条直线把A和B分开。如果有行列式0，那么数据集将在某个轴上发生折叠。因为A被B包围，所以A在任何轴上折叠都会导致部分A数据点与B混合，致使无法区分A和B。
但如果我们添加第三个隐藏单元，问题就迎刃而解了。此时，神经网络可以将数据转换成如下表示形式：
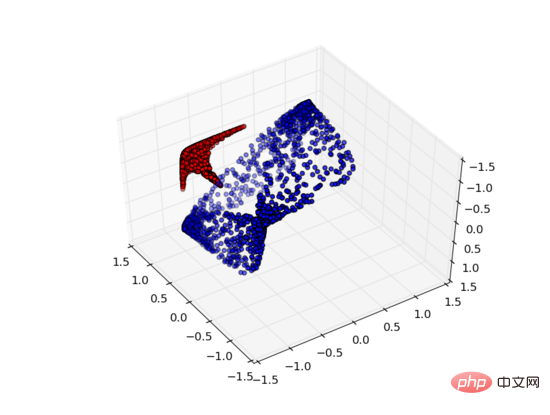
这时就可以用一个超平面来分隔A和B了。
为了更好地解释其原理，此处用一个更简单的一维数据集举例：
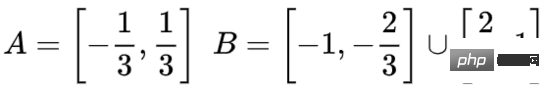
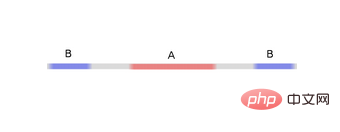
要对这个数据集进行分类，必须使用由两个或以上隐藏单元组成的层。如果使用两个隐藏单元，就可以用一条漂亮的曲线来表示数据，这样就可以用一条直线来分隔A和B：
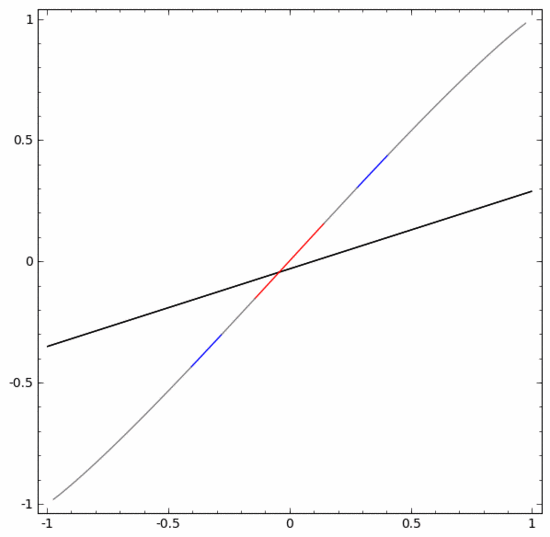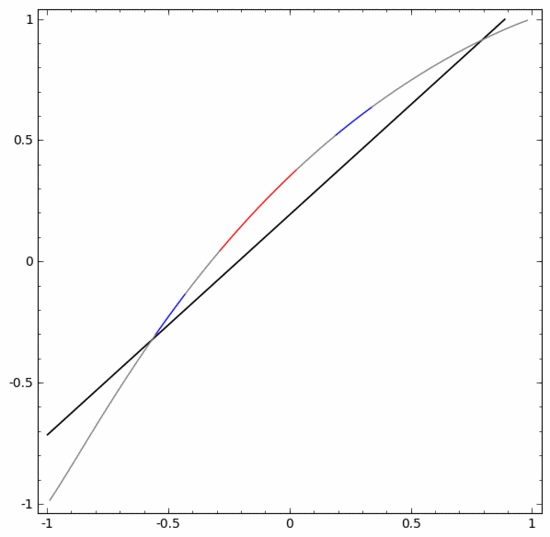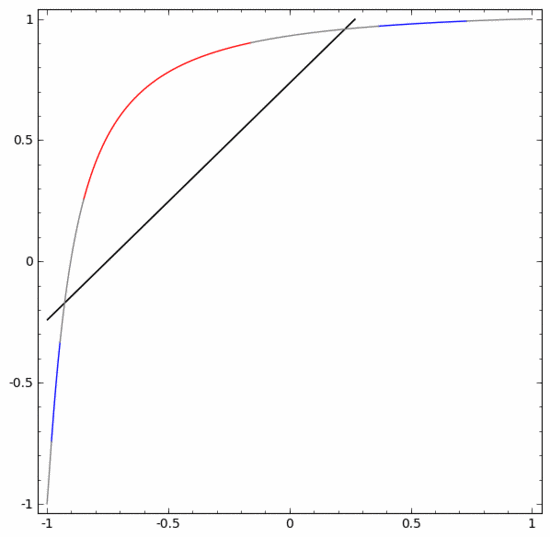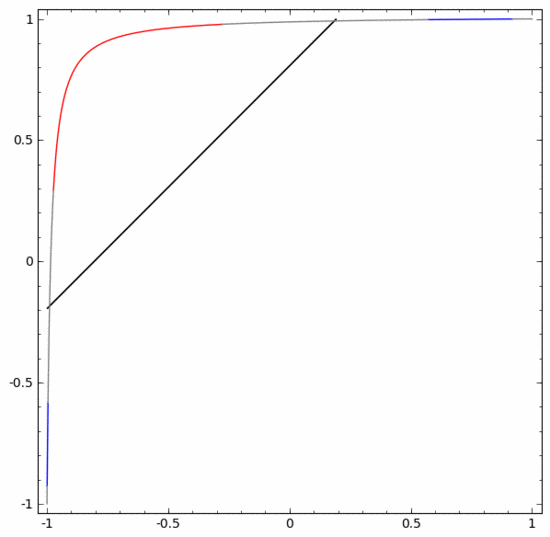
这是怎么做到的呢？当 
时，其中一个隐藏单元被激活；当 
时，另一个隐藏单元被激活。当前一个隐藏单元被激活而后一个隐藏单元未被激活时，就可以判断出这是属于A的数据点。
流形假说对处理真实世界的数据集（比如图像数据）有意义吗？我认为有意义。
流形假设是指自然数据在其嵌入空间中形成低维流形。这一假设具备理论和实验支撑。如果你相信流形假设，那么分类算法的任务就可以归结为分离一组互相纠缠的流形。
在前面的示例中，一个类完全包围了另一个类。然而，在真实世界的数据中，狗的图像流形不太可能被猫的图像流形完全包围。但是，其他更合理的拓扑情况依然可能会引发问题，下一节将会详谈。
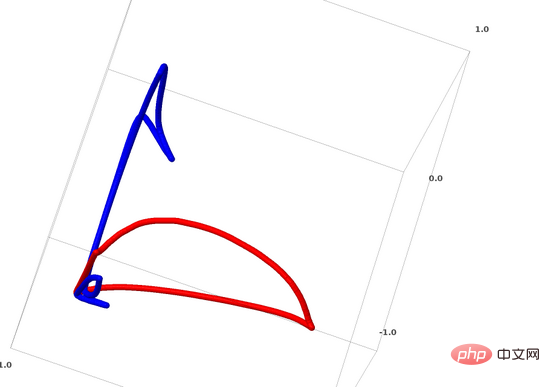
下面我将谈谈另一种有趣的数据集：两个互相链接的圆环面（tori），A 和 B。
与我们之前谈到的数据集情况类似，如果不使用n+1维度，就不能分离一个n维的数据集（n+1维度在本例中即为第4维度）。
链接问题属于拓扑学中的纽结理论。有时候，我们看到一个链接，并不能立马判断它是否是一个断链（unlink断链的意思是，虽然它们互相纠缠，但可以通过连续变形将其分离）。
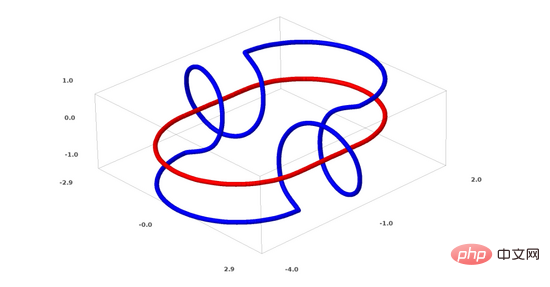
一个较简单的断链
如果隐藏层只有3个隐藏单元的神经网络可以对一个数据集进行分类，那么这个数据集就是一个断链（问题来了：从理论上讲，所有断链都可以被只有3个隐藏单元的神经网络分类吗？）。
从纽结理论的角度来看，神经网络产生的数据表示形式的连续可视化不仅仅是一个很好的动画，也是一个解开链接的过程。在拓扑学中，我们称之为原始链接和分离后的链接之间的环绕同痕（ambient isotopy）。
流形A和流形B之间的环绕同痕是一个连续函数：
每个 是X的同胚。 是特征函数， 将A映射到B。也就是说， 不断从将A映射到自身过渡到将A映射到B。
定理 ：如果同时满足以下三个条件：(1)W为非奇异；(2)可以手动排列隐藏层中神经元的顺序；(3)隐藏单元的数量大于1，那么神经网络的输入和神经网络层产生的表示形式之间有一个环绕同痕。
证明 ：我们同样一步一步来：
1. 最难的部分是线性转换。为了实现线性转换，我们需要W有一个正行列式。我们的前提是行列式为非零，如果行列式为负，我们可以通过调换两个隐藏神经元将其转化为正。正行列式矩阵的空间是路径连接的（path-connected），这就有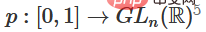
， 因此，
，
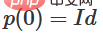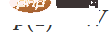。通过函数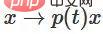
，我们可以连续地将特征函数过渡到W转换，在时间t在每个点将x与连续过渡的矩阵 相乘。
2. 可以通过函数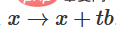
从特征函数过渡到b平移。
3. 可以通过函数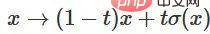
从特征函数过渡到 的逐点应用。
我猜可能有人会对下面这个问题感兴趣：能不能研发出可自动发现这种环绕同痕 （ambient isotopy）的 程序，还能自动证明某些不同链接的等效性或某些链接的可分离性。我也很想知道神经网络在这方面能不能打败目前的SOTA技术。
虽然我们现在所谈的链接形式很可能不会在现实世界的数据中出现，但现实的数据可能存在更高维度的泛化。
链接和纽结都是1维的流形，但需要4个维度才能将它们分离。同样，要分离n维的流形，就需要更高维度的空间。所有的n维流形都可以用2n+2个维度分离。
对于神经网络来说，最简单的方法就是将互缠的流形直接拉开，而且将那些缠结在一起的部分拉得越细越好。虽然这不是我们追求的根本性解决方案，但它可以实现相对较高的分类精度，达到一个相对理想的局部最小值。
这种方法会导致试图拉伸的区域出现非常高的导数。应对这一点需要采用收缩惩罚，也就是惩罚数据点的层的导数。
局部极小值对解决拓扑问题并无用处，不过拓扑问题或许可以为探索解决上述问题提供好的思路。
另一方面，如果我们只关心取得好的分类结果，那么假如流形有一小部分与另一个流形互相缠绕，这对我们来说是个问题吗？如果我们只在乎分类结果，那么这似乎不成问题。
（我的直觉认为，像这样走捷径的方法并不好，容易走进死胡同。特别是，在优化问题中，寻求局部极小值并不能真正解决问题，而如果选择一个不能真正解决问题的方案，就终将不能取得良好的性能。）
我认为标准的神经网络层并不适合操纵流形，因为它们使用的是仿射变换和逐点激活函数。
或许我们可以使用一种完全不同的神经网络层？
我脑海中浮现的一个想法是，首先，让神经网络学习一个向量场，向量场的方向是我们想要移动流形的方向：
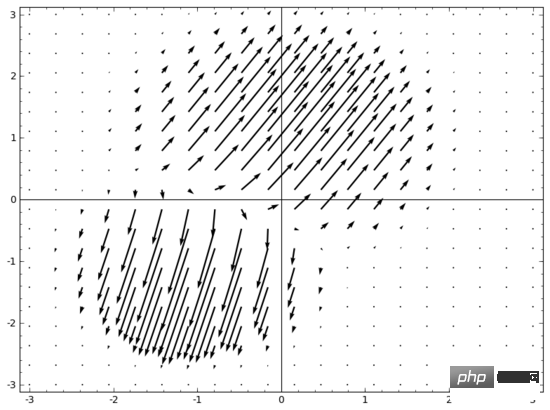
然后在此基础上变形空间：
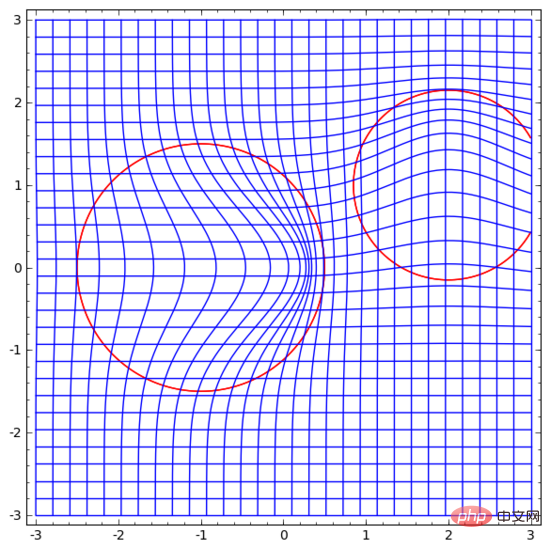
我们可以在固定点学习向量场（只需从训练集中选取一些固定点作为锚），并以某种方式进行插值。上面的向量场的形式如下：
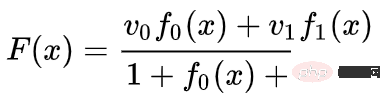
其中 和 是向量， 和 是n维高斯函数。这一想法受到径向基函数的启发。
我的另一观点是，对神经网络而言，线性可分性可能是一个过高且不合理的要求，或许使用k近邻（k-NN）会更好。然而，k-NN算法很大程度上依赖数据的表示形式，因此，需要有良好的数据表示形式才能让k-NN算法取得好结果。
在第一个实验中，我训练了一些MNIST神经网络（两层CNN，无dropout），错误率低于1%。然后，我丢弃了最后的softmax层，使用了k-NN算法，多次结果显示，错误率降低了0.1-0.2%。
不过，我感觉这种做法依然不对。神经网络仍然在尝试线性分类，只不过由于使用了k-NN算法，所以能够略微修正一些它所犯的错误，从而降低错误率。
由于（1/distance）的加权，k-NN对于它所作用的数据表示形式是可微的。因此，我们可以直接训练神经网络进行k-NN分类。这可以视为一种“最近邻”层，它的作用与softmax层类似。
我们不想为每个小批量反馈整个训练集，因为这样计算成本太高。我认为一个很好的方法是，根据小批量中其他元素的类别对小批量中的每个元素进行分类，给每个元素赋予（1/(与分类目标的距离)）的权重。
遗憾的是，即使使用复杂的架构，使用k-NN算法也只能把错误率降低至4-5%，而使用简单的架构错误率则更高。不过，我并未在超参数方面下太多工夫。
但我还是很喜欢k-NN算法，因为它更适合神经网络。我们希望同一流形的点彼此更靠近，而不是执着于用超平面把流形分开。这相当于使单个流形收缩，同时使不同类别的流形之间的空间变大。这样就把问题简化了。
数据的某些拓扑特性可能导致这些数据不能使用低维神经网络来进行线性分离（无论神经网络深度如何）。即使在技术可行的情况下，例如螺旋，用低维神经网络也非常难以实现分离。
为了对数据进行精确分类，神经网络有时需要更宽的层。此外，传统的神经网络层不适合操纵流形；即使人工设置权重，也很难得到理想的数据转换表示形式。新的神经网络层或许能起到很好的辅助作用，特别是从流形角度理解机器学习启发得出的新神经网络层。
以上是18张图直观理解神经网络、流形和拓扑的详细内容。更多信息请关注PHP中文网其他相关文章！
