js基本算法:冒泡排序,二分查找
知识扩充:
时间复杂度:算法的时间复杂度是一个函数,描述了算法的运行时间。时间复杂度越低,效率越高。
自我理解:一个算法,运行了几次时间复杂度就为多少,如运行了n次,则时间复杂度为O(n)。
1.冒泡排序
解析:1.比较相邻的两个元素,如果前一个比后一个大,则交换位置。
2.第一轮的时候最后一个元素应该是最大的一个。
3.按照步骤一的方法进行相邻两个元素的比较,这个时候由于最后一个元素已经是最大的了,所以最后一个元素不用比较。
function sort(elements){
for(var i=0;i<elements.length-1;i++){
for(var j=0;j<elements.length-i-1;j++){
if(elements[j]>elements[j+1]){
var swap=elements[j];
elements[j]=elements[j+1];
elements[j+1]=swap;
}
}
}
}
var elements = [3, 1, 5, 7, 2, 4, 9, 6, 10, 8];
console.log('before: ' + elements);
sort(elements);
console.log(' after: ' + elements);2.快速排序
解析:快速排序是对冒泡排序的一种改进,第一趟排序时将数据分成两部分,一部分比另一部分的所有数据都要小。然后递归调用,在两边都实行快速排序。
function quickSort(elements) {
if (elements.length <= 1) { return elements; }
var pivotIndex = Math.floor(elements.length / 2);
var pivot = elements.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < elements.length; i++){
if (elements[i] < pivot) {
left.push(elements[i]);
} else {
right.push(elements[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
var elements=[5,6,2,1,3,8,7,1.2,5.5,4.5];
alert(quickSort(elements));3.插入排序
解析:
(1) 从第一个元素开始,该元素可以认为已经被排序
(2) 取出下一个元素,在已经排序的元素序列中从后向前扫描
(3) 如果该元素(已排序)大于新元素,将该元素移到下一位置
(4) 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
(5)将新元素插入到下一位置中
(6) 重复步骤2
insertSort: function(elements) {
var i = 1,
j, step, key, len = elements.length;
for (; i < len; i++) {
step = j = i;
key = elements[j];
while (--j > -1) {
if (elements[j] > key) {
elements[j + 1] = elements[j];
} else {
break;
}
}
elements[j + 1] = key;
}
return elements;
}2.二分查找
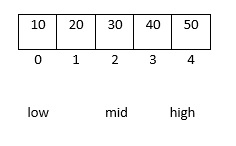
解析:二分查找,也为折半查找。首先要找到一个中间值,通过与中间值比较,大的放又,小的放在左边。再在两边中寻找中间值,持续以上操作,直到找到所在位置为止。
(1)递归方法
function binarySearch(data,item,start,end){
var end=end || data.length-1;
var start=start || 0;
var m=Math.floor((start+end)/2);
if(item==data[m]){
return m;
}else if(item<data[m]){
return binarySearch(data,item,start,m-1) //递归调用
}else{
return binarySearch(data,item,m+1,end);
}
return false;
}
var arr=[34,12,5,123,2,745,32,4];
binary(arr,5);(2)非递归方法
function binarySearch(data, item){
var h = data.length - 1,
l = 0;
while(l <= h){
var m = Math.floor((h + l) / 2);
if(data[m] == item){
return m;
}
if(item > data[m]){
l = m + 1;
}else{
h = m - 1;
}
}
return false;
}
var arr=[34,12,5,123,2,745,32,4];
binarySearch(arr,5);
热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 如何使用C#编写二分查找算法
Sep 19, 2023 pm 12:42 PM
如何使用C#编写二分查找算法
Sep 19, 2023 pm 12:42 PM
如何使用C#编写二分查找算法二分查找算法是一种高效的查找算法,它在有序数组中查找特定元素的位置,时间复杂度为O(logN)。在C#中,我们可以通过以下几个步骤来编写二分查找算法。步骤一:准备数据首先,我们需要准备一个已经排好序的数组作为查找的目标数据。假设我们要在数组中查找特定元素的位置。int[]data={1,3,5,7,9,11,13
 使用二分查找算法找到一个数的立方根的Java程序
Aug 28, 2023 pm 01:33 PM
使用二分查找算法找到一个数的立方根的Java程序
Aug 28, 2023 pm 01:33 PM
立方根是一个整数值,当它自己连续乘以自己三次时,得到原始数值。在本文中,我们将编写一个使用二分搜索来找到一个数的立方根的Java程序。找到一个数的立方根是二分搜索算法的一个应用之一。在本文中,我们将详细讨论如何使用二分搜索来计算立方根。输入-输出示例Example-1:Input:64Output:4如,64的立方根为4,输出为4。Example-2:Input:216Output:6如,216的立方根为6,输出为6。二分查找二分搜索是一种用于查找元素(即排序数组中的键)的算法。二进制算法的工作
 使用C语言编写的二分查找程序,使用pthread进行多线程处理
Aug 26, 2023 pm 12:45 PM
使用C语言编写的二分查找程序,使用pthread进行多线程处理
Aug 26, 2023 pm 12:45 PM
我们知道二分查找方法是一种最适合和有效的排序算法。这个算法适用于已排序的序列。算法很简单,它只是从中间找到元素,然后将列表分成两部分,并向左子列表或右子列表移动。我们知道它的算法。现在我们将看到如何在多线程环境中使用二分查找技术。线程的数量取决于系统中存在的核心数。让我们看一下代码以了解思路。示例#include<iostream>#defineMAX16#defineMAX_THREAD4usingnamespacestd;//placearr,keyandothervariabl
 如何使用二分查找算法在C语言中找到数组中的最小元素?
Aug 25, 2023 pm 08:37 PM
如何使用二分查找算法在C语言中找到数组中的最小元素?
Aug 25, 2023 pm 08:37 PM
C编程语言提供了两种搜索技术。它们如下所示:线性搜索二分搜索二分搜索这种方法只适用于有序列表。给定列表被分成两个相等的部分。给定的关键字与列表的中间元素进行比较。在这里,可能会发生三种情况,如下所示:如果中间元素与关键字匹配,则搜索将在此成功结束如果中间元素大于关键字,则搜索将在左侧分区进行。如果中间元素小于关键字,则搜索将在右侧分区进行。输入(i/p)-未排序的元素列表,关键字。输出(o/p)-成功-如果找到关键字失败-否则key=20mid=(low+high)/2程序1以下是使用二分查找在
 如何使用Python实现二分查找算法?
Sep 20, 2023 pm 01:24 PM
如何使用Python实现二分查找算法?
Sep 20, 2023 pm 01:24 PM
如何使用Python实现二分查找算法?二分查找算法,也称为折半查找算法,是一种高效的查找算法。它适用于有序的数组或列表,通过将目标值与数组中间位置的元素进行比较,从而缩小查找范围。下面将介绍如何在Python中实现二分查找算法,并提供具体的代码示例。算法思路:将目标值与数组中间位置的元素进行比较;如果相等,则返回元素位置;如果目标值大于中间位置的元素,则在右
 如何使用java实现二分查找算法
Sep 19, 2023 pm 12:57 PM
如何使用java实现二分查找算法
Sep 19, 2023 pm 12:57 PM
如何使用Java实现二分查找算法二分查找算法是一种高效的查找方法,适用于已排序的数组。它的基本思想是不断缩小查找范围,将查找值与数组中间的元素进行比较,并根据比较结果决定继续查找左半部分还是右半部分,直到找到目标元素或查找范围缩小为空。下面我们来具体介绍如何用Java实现二分查找算法。步骤一:实现二分查找方法publicclassBinarySearch
 PHP算法解析:如何使用二分查找算法在有序数组中快速定位元素?
Sep 19, 2023 pm 01:14 PM
PHP算法解析:如何使用二分查找算法在有序数组中快速定位元素?
Sep 19, 2023 pm 01:14 PM
PHP算法解析:如何使用二分查找算法在有序数组中快速定位元素?概述:二分查找算法是一种高效的查找算法,它适用于有序数组中查找特定元素。本文将详细介绍二分查找算法的原理,并给出PHP代码示例。原理:二分查找算法通过反复将查找范围缩小一半,从而快速定位目标元素。其流程如下:首先,将查找范围缩小为数组的开头和结尾;然后,计算中间元素的索引,将其与目标元素进行比较;
 在C程序中,使用二分查找算法来搜索有理数,而不使用浮点数算术
Aug 27, 2023 pm 06:05 PM
在C程序中,使用二分查找算法来搜索有理数,而不使用浮点数算术
Aug 27, 2023 pm 06:05 PM
在这个问题中,我们得到了一个有理数的排序数组。我们必须使用二分搜索算法来搜索该有理数数组的给定元素,而不使用浮点运算。有理数是以p/q形式表示的数字,其中p和q都是整数。例如,⅔、⅕。二分搜索是一种搜索技术,通过查找数组的中间来查找元素。用于查找使用二分法搜索有理数排序数组中的元素,其中不允许浮点运算。我们将比较分子和分母,以找出哪个元素更大或哪个元素是要找到的元素。示例让我们为此创建一个程序,#include<stdio.h>structRational{ &am






