到达拐角所需清除的障碍物最少
2290。最少清除障碍物才能到达拐角
难度:难
主题:数组、广度优先搜索、图、堆(优先级队列)、矩阵、最短路径
给你一个 0 索引 大小为 m x n 的 2D 整数数组网格。每个单元格都有两个值之一:
- 0 代表空单元格,
- 1 代表可以移除的障碍物。
您可以在空单元格之间向上、向下、向左或向右移动。
将最小个障碍物返回到移除,这样你就可以从左上角(0, 0)移动到右下角角 (m - 1, n - 1).
示例1:

- 输入: grid = [[0,1,1],[1,1,0],[1,1,0]]
- 输出: 2
-
解释:我们可以移除 (0, 1) 和 (0, 2) 处的障碍物,创建一条从 (0, 0) 到 (2, 2) 的路径。
- 可以证明我们需要移除至少 2 个障碍物,因此我们返回 2。
- 请注意,可能还有其他方法可以移除 2 个障碍物来创建一条路径。
示例2:
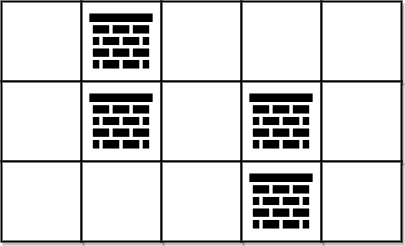
- 输入: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
- 输出: 0
- 解释:我们可以在不移除任何障碍的情况下从 (0, 0) 移动到 (2, 4),因此我们返回 0。
约束:
- m == grid.length
- n == grid[i].length
- 1 5
- 2 5
- grid[i][j] 为 0 或 1。
- 网格[0][0] == 网格[m - 1][n - 1] == 0
提示:
- 将网格建模为图形,其中单元格是节点,边是相邻单元格之间的。有障碍物的单元格的边缘的成本为 1,所有其他边缘的成本为 0。
- 你能使用0-1广度优先搜索或Dijkstra算法吗?
解决方案:
我们需要使用图表来模拟这个问题,其中网格中的每个单元格都是一个节点。目标是从左上角 (0, 0) 导航到右下角 (m-1, n-1),同时最大限度地减少我们需要移除的障碍物 (1s) 的数量。
方法:
-
图形表示:
- 网格中的每个单元格都是一个节点。
- 相邻单元格之间的移动(上、下、左、右)被视为边缘。
- 如果一条边穿过带有 1(障碍物)的单元格,则成本为 1(移除障碍物),如果它穿过 0(空单元格),则成本为 0。
-
算法选择:
- 由于我们需要最小化移除的障碍物数量,因此我们可以使用 0-1 BFS(使用双端队列的广度优先搜索)或 Dijkstra 算法 以及优先级队列。
- 0-1 BFS 适合这里,因为每条边的成本为 0 或 1。
-
0-1 BFS:
- 我们使用deque(双端队列)来处理不同成本的节点:
- 将成本为 0 的单元推到双端队列的前面。
- 将成本为 1 的单元推到双端队列的后面。
- 这个想法是探索网格并始终先扩展不需要移除障碍物的路径,并且仅在必要时移除障碍物。
- 我们使用deque(双端队列)来处理不同成本的节点:
让我们用 PHP 实现这个解决方案:2290。到达拐角所需清除的最小障碍物
<?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function minimumObstacles($grid) {
...
...
...
/**
* go to ./solution.php
*/
}
// Test Case 1
$grid1 = [
[0, 1, 1],
[1, 1, 0],
[1, 1, 0]
];
echo minimumObstacles($grid1) . PHP_EOL; // Output: 2
// Test Case 2
$grid2 = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0]
];
echo minimumObstacles($grid2) . PHP_EOL; // Output: 0
?>
解释:
-
输入解析:
- 网格被视为二维数组。
- 计算行和列以进行边界检查。
-
双端队列实现:
- SplDoublyLinkedList用于模拟双端队列。支持在前面(unshift)或后面(push)添加元素。
-
已访问数组:
- 跟踪已访问过的单元格以避免冗余处理。
-
0-1 BFS 逻辑:
- 从 (0, 0) 开始,成本为 0。
- 对于每个相邻单元格:
- 如果为空(grid[nx][ny] == 0),则以相同的成本将其添加到双端队列的前面。
- 如果它是一个障碍物 (grid[nx][ny] == 1),则将其添加到双端队列的后面,并增加成本。
-
返回结果:
- 到达右下角时,返回费用。
- 如果不存在有效路径(尽管问题保证有一个),则返回 -1。
复杂:
- 时间复杂度: O(m x n),其中 m 是行数,n 是列数。每个单元格都会被处理一次。
- 空间复杂度: O(m x n),对于访问的数组和双端队列。
此实现在给定的限制内有效地工作。
联系链接
如果您发现本系列有帮助,请考虑在 GitHub 上给 存储库 一个星号或在您最喜欢的社交网络上分享该帖子?。您的支持对我来说意义重大!
如果您想要更多类似的有用内容,请随时关注我:
- 领英
- GitHub
以上是到达拐角所需清除的障碍物最少的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 在PHP API中说明JSON Web令牌(JWT)及其用例。
Apr 05, 2025 am 12:04 AM
在PHP API中说明JSON Web令牌(JWT)及其用例。
Apr 05, 2025 am 12:04 AM
JWT是一种基于JSON的开放标准,用于在各方之间安全地传输信息,主要用于身份验证和信息交换。1.JWT由Header、Payload和Signature三部分组成。2.JWT的工作原理包括生成JWT、验证JWT和解析Payload三个步骤。3.在PHP中使用JWT进行身份验证时,可以生成和验证JWT,并在高级用法中包含用户角色和权限信息。4.常见错误包括签名验证失败、令牌过期和Payload过大,调试技巧包括使用调试工具和日志记录。5.性能优化和最佳实践包括使用合适的签名算法、合理设置有效期、
 会话如何劫持工作,如何在PHP中减轻它?
Apr 06, 2025 am 12:02 AM
会话如何劫持工作,如何在PHP中减轻它?
Apr 06, 2025 am 12:02 AM
会话劫持可以通过以下步骤实现:1.获取会话ID,2.使用会话ID,3.保持会话活跃。在PHP中防范会话劫持的方法包括:1.使用session_regenerate_id()函数重新生成会话ID,2.通过数据库存储会话数据,3.确保所有会话数据通过HTTPS传输。
 PHP 8.1中的枚举(枚举)是什么?
Apr 03, 2025 am 12:05 AM
PHP 8.1中的枚举(枚举)是什么?
Apr 03, 2025 am 12:05 AM
PHP8.1中的枚举功能通过定义命名常量增强了代码的清晰度和类型安全性。1)枚举可以是整数、字符串或对象,提高了代码可读性和类型安全性。2)枚举基于类,支持面向对象特性,如遍历和反射。3)枚举可用于比较和赋值,确保类型安全。4)枚举支持添加方法,实现复杂逻辑。5)严格类型检查和错误处理可避免常见错误。6)枚举减少魔法值,提升可维护性,但需注意性能优化。
 描述扎实的原则及其如何应用于PHP的开发。
Apr 03, 2025 am 12:04 AM
描述扎实的原则及其如何应用于PHP的开发。
Apr 03, 2025 am 12:04 AM
SOLID原则在PHP开发中的应用包括:1.单一职责原则(SRP):每个类只负责一个功能。2.开闭原则(OCP):通过扩展而非修改实现变化。3.里氏替换原则(LSP):子类可替换基类而不影响程序正确性。4.接口隔离原则(ISP):使用细粒度接口避免依赖不使用的方法。5.依赖倒置原则(DIP):高低层次模块都依赖于抽象,通过依赖注入实现。
 在PHPStorm中如何进行CLI模式的调试?
Apr 01, 2025 pm 02:57 PM
在PHPStorm中如何进行CLI模式的调试?
Apr 01, 2025 pm 02:57 PM
在PHPStorm中如何进行CLI模式的调试?在使用PHPStorm进行开发时,有时我们需要在命令行界面(CLI)模式下调试PHP�...
 如何用PHP的cURL库发送包含JSON数据的POST请求?
Apr 01, 2025 pm 03:12 PM
如何用PHP的cURL库发送包含JSON数据的POST请求?
Apr 01, 2025 pm 03:12 PM
使用PHP的cURL库发送JSON数据在PHP开发中,经常需要与外部API进行交互,其中一种常见的方式是使用cURL库发送POST�...
 解释PHP中的晚期静态绑定(静态::)。
Apr 03, 2025 am 12:04 AM
解释PHP中的晚期静态绑定(静态::)。
Apr 03, 2025 am 12:04 AM
静态绑定(static::)在PHP中实现晚期静态绑定(LSB),允许在静态上下文中引用调用类而非定义类。1)解析过程在运行时进行,2)在继承关系中向上查找调用类,3)可能带来性能开销。







