numpy&#s einsum 的不合理用处

介绍

我想向您介绍Python中最有用的方法，np.einsum。

使用 np.einsum（以及 Tensorflow 和 JAX 中的对应项），您可以以极其清晰和简洁的方式编写复杂的矩阵和张量运算。 我还发现它的清晰性和简洁性减轻了很多使用张量带来的精神负担。

而且它实际上学习和使用起来相当简单。 其工作原理如下：

在 np.einsum 中，您有一个下标字符串参数，并且有一个或多个操作数：

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

下标参数是一种“迷你语言”，它告诉 numpy 如何操作和组合操作数的轴。 刚开始读起来有点困难，但是掌握窍门后也不错。

单一操作数

第一个示例，让我们使用 np.einsum 交换矩阵 A 的轴（也称为转置）：

M = np.einsum('ij->ji', A)

字母 i 和 j 绑定到 A 的第一个和第二个轴。Numpy 按照字母出现的顺序将字母绑定到轴，但如果你是显式的，numpy 并不关心你使用什么字母。 例如，我们可以使用 a 和 b，其工作方式相同：

M = np.einsum('ab->ba', A)

但是，您必须提供与操作数中的轴一样多的字母。 A 中有两个轴，因此您必须提供两个不同的字母。 下一个示例不会工作，因为下标公式只有一个字母要绑定，i：

# broken
M = np.einsum('i->i', A)

另一方面，如果操作数确实只有一个轴（即，它是一个向量），那么单字母下标公式就可以正常工作，尽管它不是很有用，因为它使向量成为原样：

m = np.einsum('i->i', a)

对轴求和

但是这个操作呢？ 右边没有 i。 这有效吗？

c = np.einsum('i->', a)

令人惊讶的是，是的！

这是理解 np.einsum 本质的第一个关键：如果一个轴从右侧省略，那么该轴对求和。

代码：

c = 0
I = len(a)
for i in range(I):
   c += a[i]

求和行为不限于单个轴。 例如，您可以使用以下下标公式同时对两个轴求和： c = np.einsum('ij->', A):

这是两个轴上相应的 Python 代码：

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

但它并不止于此 - 我们可以发挥创造力，对一些轴进行求和，而忽略其他轴。 例如： np.einsum('ij->i', A) 对矩阵 A 的行求和，留下长度为 j 的行和向量：

代码：

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

同样，np.einsum('ij->j', A) 对 A 中的列进行求和。

代码：

M = np.einsum('ij->ji', A)

两个操作数

我们用单个操作数可以做的事情是有限的。 使用两个操作数，事情会变得更加有趣（并且有用）。

假设您有两个向量 a = [a_1, a_2, ... ] 和 b = [a_1, a_2, ...]。

如果 len(a) === len(b)，我们可以这样计算内积（也称为点积）：

M = np.einsum('ab->ba', A)

这里同时发生两件事：

1. 因为 i 与 a 和 b 都绑定，所以 a 和 b 会“排列”然后相乘：a[i] * b[i]。
2. 因为索引 i 被排除在右侧，所以对轴 i 进行求和以消除它。

如果将（1）和（2）放在一起，您将得到经典的内积。

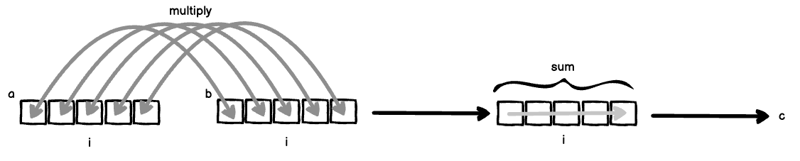
代码：

# broken
M = np.einsum('i->i', A)

现在，假设我们没有从下标公式中省略i，我们将所有a[i]和b[i]相乘，并且不总和除以i：

m = np.einsum('i->i', a)

代码：

c = np.einsum('i->', a)

这也称为逐元素乘法（或矩阵的哈达玛积），通常通过 numpy 方法 np.multiply 完成。

下标公式还有第三种变体，称为外积。

c = 0
I = len(a)
for i in range(I):
   c += a[i]

在此下标公式中，a 和 b 的轴绑定到单独的字母，因此被视为单独的“循环变量”。 因此，C 对于所有 i 和 j 都有条目 a[i] * b[j]，排列成矩阵。

代码：

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

三个操作数

将外积更进一步，这是一个三操作数版本：

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

我们的三操作数外积的等效 Python 代码是：

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

更进一步，没有什么可以阻止我们省略轴来对它们求和，除了转置通过在右侧写ki而不是ik来计算结果->:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

等效的 Python 代码为：

M = np.einsum('ij->ji', A)

现在我希望您可以开始了解如何轻松地指定复杂的张量运算。 当我更广泛地使用 numpy 时，我发现每当我必须实现复杂的张量运算时，我都会使用 np.einsum。

根据我的经验，np.einsum 使以后的代码阅读更加容易 - 我可以轻松地直接从下标读出上述操作：“三个向量的外积，中间轴相加，最终结果转置”。 如果我必须阅读一系列复杂的 numpy 运算，我可能会发现自己张口结舌。

一个实际的例子

举一个实际的例子，让我们实现法学硕士的核心方程，来自经典论文“注意力就是你所需要的”。

等式。 1 描述注意力机制：

我们将把注意力集中在这个词上 $Q{K}^T$QKT ，因为 softmax 无法通过 np.einsum 和缩放因子计算 $\frac{1}{\sqrt{d_k}}$dk​​1 ​ 申请起来很简单。

的 $Q{K}^T$QKT term 表示 m 个查询与 n 个键的点积。 Q 是 m 个 d 维行向量堆叠成矩阵的集合，因此 Q 的形状为 md。同样，K 是 n 个 d 维行向量堆叠成矩阵的集合，因此 K 的形状为 md。

单个 Q 和 K 之间的乘积可写为：

np.einsum('md,nd->mn', Q, K)

请注意，由于我们编写下标方程的方式，我们避免了在矩阵乘法之前转置 K！

所以，这看起来非常简单 - 事实上，它只是一个传统的矩阵乘法。 然而，我们还没有完成。 注意力就是你所需要的使用多头注意力，这意味着我们确实有k这样的矩阵乘法在Q矩阵和K矩阵的索引集合上同时发生.

为了让事情更清楚一些，我们可以将产品重写为 $Q_i{K}_i^T$Q我​K 我T​ .

这意味着我们对于 Q 和 K 都有一个额外的轴 i。

更重要的是，如果我们处于训练环境中，我们可能正在执行批量这样的多头注意力操作。

因此大概想要沿着批处理轴 b 对一批示例执行操作。 因此，完整的产品将类似于：

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

我将跳过这里的图表，因为我们正在处理 4 轴张量。 但是您也许可以想象“堆叠”早期的图表以获得我们的多头轴 i，然后“堆叠”这些“堆栈”以获得我们的批处理轴 b。

我很难理解如何使用其他 numpy 方法的任意组合来实现这样的操作。 然而，通过一些检查，就很清楚发生了什么：在一个批处理中，在矩阵 Q 和 K 的集合上，执行矩阵乘法 Qt(K).

现在，这不是很棒吗？

无耻的插头

在创始人模式磨练了一年之后，我正在找工作。 我在各种技术领域和编程语言方面拥有超过 15 年的经验，并且还有管理团队的经验。 数学和统计学是重点领域。 DM 我，让我们谈谈！

以上是numpy&#s einsum 的不合理用处的详细内容。更多信息请关注PHP中文网其他相关文章！