合併兩棵樹後求最小直徑

3203。合併兩棵樹後求最小直徑

難度：難

主題：樹、深度優先搜尋、廣度優先搜尋、圖

存在兩棵無向樹，分別有n和m個節點，編號分別為0到n - 1和0到m - 1。給定兩個二維整數數組edges1和edges2，長度分別為n - 1和m - 1，其中edges1[i] = [a_i, b_i]表示有是第一棵樹中節點a_i 和b_i 之間的邊，edges2[i] = [u_i, v_i] 表示第二棵樹中的節點u_i 和v_i 之間有一條邊。

您必須使用邊將第一棵樹中的一個節點與第二棵樹中的另一個節點連接起來。

回傳所得樹的最小值可能的直徑。

樹的直徑是樹中任兩個節點之間最長路徑的長度。

範例1：

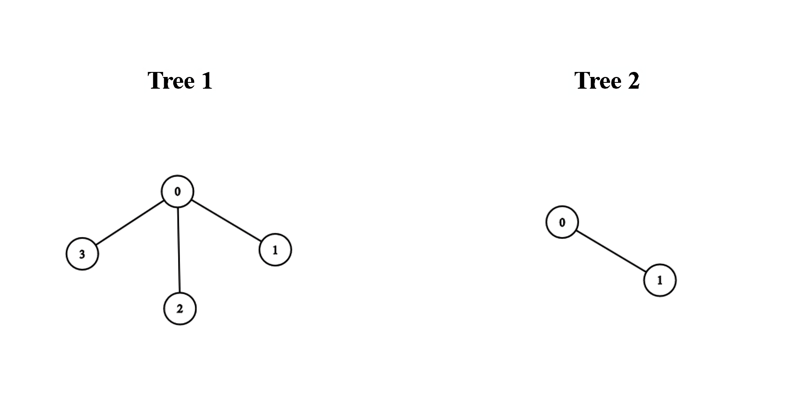
• 輸入： Edges1 = [[0,1],[0,2],[0,3]], Edges2 = [[0,1]]
• 輸出： 3
• 說明：將第一棵樹的節點 0 與第二棵樹的任意節點連接，我們可以得到一棵直徑為 3 的樹。

範例2：

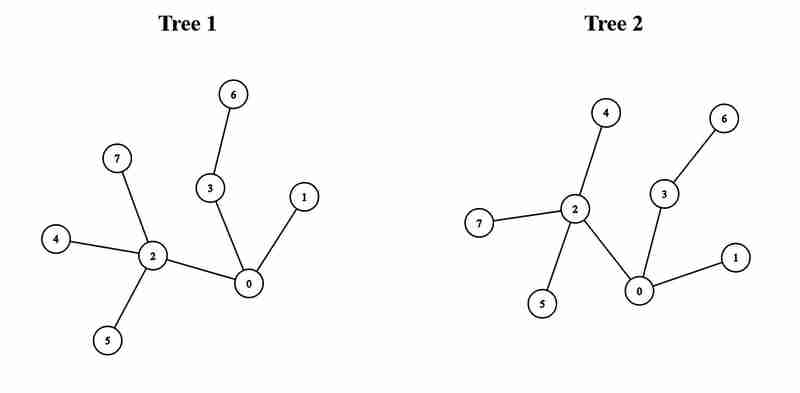
• 輸入：edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2, 7]]，邊2 = [[0,1]，[0,2]，[0,3]，[2,4]，[2,5]，[3,6]，[2,7]]
• 輸出： 5
• 說明：將第一棵樹的節點 0 與第二棵樹的節點 0 連接起來，我們可以得到一棵直徑為 5 的樹。

約束：

• 1 5
• edges1.length == n - 1
• edges2.length == m - 1
• edges1[i].length == Edges2[i].length == 2
• edges1[i] = [a_i, b_i]
• 0 i, b_i
• edges2[i] = [u_i, v_i]
• 0 i, v_i
• 產生輸入，使得edge1和edge2代表有效的樹。

提示：

1. 假設我們將tree1中的節點a與tree2中的節點b連結起來。產生的樹的直徑長度將是以下 3 個值中最大的一個：
   1. 樹的直徑1.
   2. 樹的直徑2.
   3. 從節點 a 開始且完全在樹 1 內的最長路徑的長度 從節點 b 開始且完全在樹 2 內的最長路徑的長度 1.
   4. 第三個值中新增的一個是由於我們在樹 1 和 2 之間添加了額外的邊。
2. 無論我們選擇 a 和 b，值 1 和 2 都是恆定的。因此，我們需要以最小化值 3 的方式選擇 a 和 b。
3. 如果我們選擇最佳的 a 和 b，它們將分別位於 Tree 1 和 Tree 2 的直徑內。我們到底該選擇哪些直徑的節點？
4. a 是樹 1 的直徑中心，b 是樹 2 的直徑中心。

解：

我們需要逐步解決它，重點是了解如何計算樹的直徑以及連接兩棵樹如何影響總直徑。

解決步驟：

1. 求每棵樹的直徑:

   • 樹的直徑是任兩個節點之間最長的路徑。為了找到它，我們可以使用以下兩個步驟：
     1. 從任意節點執行 BFS（或 DFS）以找到最遠的節點（我們將此節點稱為 A）。
     2. 從A開始再進行一次BFS（或DFS），找出距離A最遠的節點（我們稱這個節點為B），A到B的距離就是樹的直徑。

2. 確定最佳連接節點:

   • 從問題的提示來看，連接兩棵樹時最小化附加直徑的最佳方法是連接兩棵樹的直徑中心。這將最大限度地減少新邊造成的最長路徑。
   • 樹直徑中的最佳節點通常是“中心”，可以透過從直徑的端點執行 BFS 並找到最長路徑的中間來找到它。

3. 最小化總直徑:

   • 一旦我們找到兩棵樹的中心，新的直徑就是以下值中的最大值：
     • 樹 1 的直徑。
     • 樹 2 的直徑。
     • 樹 1 中的最長路徑、樹 2 中最長的路徑、新連接邊 1 的總和。

讓我們用 PHP 實作這個解：3203。合併兩棵樹後求最小直徑

解釋：

1. BFS 輔助函數：bfs 函數計算距離給定起始節點最遠的節點，並傳回距離陣列和找到的最遠節點。這對於計算樹的直徑至關重要。

2. 取得直徑和中心：getDiameterAndCenter 函數找出樹的直徑及其中心。合併兩棵樹時，樹的中心對於最小化新樹的直徑至關重要。

3. 主要解：

   • 我們先為兩棵樹建立鄰接表。
   • 我們計算兩棵樹的直徑和中心。
   • 我們從兩棵樹的中心執行 BFS，以獲得每棵樹內的最長路徑。
   • 最後，我們計算三個值中的最大值，得到合併樹的最小直徑。

時間複雜度：

• 建立鄰接表：O(n·m)
• BFS 遍歷：O(n·m)
• 總體時間複雜度為 O(n m)，對於 10⁵.
輸入大小限制是有效的

這種方法確保我們在合併兩棵樹時找到盡可能小的直徑。

聯絡連結

如果您發現本系列有幫助，請考慮在 GitHub 上給 存儲庫 一個星號或在您最喜歡的社交網絡上分享該帖子？ 。您的支持對我來說意義重大！

如果您想要更多類似的有用內容，請隨時關注我：

• 領英
• GitHub

以上是合併兩棵樹後求最小直徑的詳細內容。更多資訊請關注PHP中文網其他相關文章！