这篇文章主要介绍了python编程通过蒙特卡洛法计算定积分详解,具有一定借鉴价值,需要的朋友可以参考下。
想当初,考研的时候要是知道有这么个好东西,计算定积分。。。开玩笑,那时候计算定积分根本没有这么简单的。但这确实给我打开了一种思路,用编程语言去解决更多更复杂的数学问题。下面进入正题。
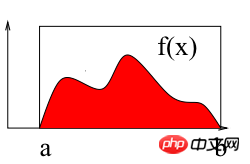
如上图所示,计算区间[a b]上f(x)的积分即求曲线与X轴围成红色区域的面积。下面使用蒙特卡洛法计算区间[2 3]上的定积分:∫(x2+4*x*sin(x))dx
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 + 4*x*np.sin(x)
def intf(x):
return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;
b = 3;
# use N draws
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
# 蒙特卡洛法计算定积分:面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
Imc[N]= (b-a) * np.sum(Y)/ N;
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()>>>
Monte Carlo estimation= 11.8181144118 Exact number= 11.8113589251
立即学习“Python免费学习笔记(深入)”;

从上图可以看出,随着采样点数的增加,计算误差逐渐减小。想要提高模拟结果的精确度有两个途径:其一是增加试验次数N;其二是降低方差σ2. 增加试验次数势必使解题所用计算机的总时间增加,要想以此来达到提高精度之目的显然是不合适的。下面来介绍重要抽样法来减小方差,提高积分计算的精度。
重要性抽样法的特点在于,它不是从给定的过程的概率分布抽样,而是从修改的概率分布抽样,使对模拟结果有重要作用的事件更多出现,从而提高抽样效率,减少花费在对模拟结果无关紧要的事件上的计算时间。比如在区间[a b]上求g(x)的积分,若采用均匀抽样,在函数值g(x)比较小的区间内产生的抽样点跟函数值较大处区间内产生的抽样点的数目接近,显然抽样效率不高,可以将抽样概率密度函数改为f(x),使f(x)与g(x)的形状相近,就可以保证对积分计算贡献较大的抽样值出现的机会大于贡献小的抽样值,即可以将积分运算改写为:
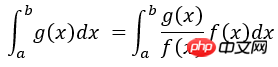
x是按照概率密度f(x)抽样获得的随机变量,显然在区间[a b]内应该有:
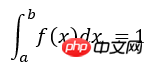
因此,可容易将积分值I看成是随机变量 Y = g(x)/f(x)的期望,式子中xi是服从概率密度f(x)的采样点
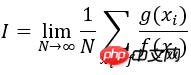
下面的例子采用一个正态分布函数f(x)来近似g(x)=sin(x)*x,并依据正态分布选取采样值计算区间[0 pi]上的积分个∫g(x)dx
# -*- coding: utf-8 -*-
# Example: Calculate ∫sin(x)xdx
# The function has a shape that is similar to Gaussian and therefore
# we choose here a Gaussian as importance sampling distribution.
from scipy import stats
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
mu = 2;
sig =.7;
f = lambda x: np.sin(x)*x
infun = lambda x: np.sin(x)-x*np.cos(x)
p = lambda x: (1/np.sqrt(2*np.pi*sig**2))*np.exp(-(x-mu)**2/(2.0*sig**2))
normfun = lambda x: norm.cdf(x-mu, scale=sig)
plt.figure(figsize=(18,8)) # set the figure size
# range of integration
xmax =np.pi
xmin =0
# Number of draws
N =1000
# Just want to plot the function
x=np.linspace(xmin, xmax, 1000)
plt.subplot(1,2,1)
plt.plot(x, f(x), 'b', label=u'Original $x\sin(x)$')
plt.plot(x, p(x), 'r', label=u'Importance Sampling Function: Normal')
plt.xlabel('x')
plt.legend()
# =============================================
# EXACT SOLUTION
# =============================================
Iexact = infun(xmax)-infun(xmin)
print Iexact
# ============================================
# VANILLA MONTE CARLO
# ============================================
Ivmc = np.zeros(1000)
for k in np.arange(0,1000):
x = np.random.uniform(low=xmin, high=xmax, size=N)
Ivmc[k] = (xmax-xmin)*np.mean(f(x))
# ============================================
# IMPORTANCE SAMPLING
# ============================================
# CHOOSE Gaussian so it similar to the original functions
# Importance sampling: choose the random points so that
# more points are chosen around the peak, less where the integrand is small.
Iis = np.zeros(1000)
for k in np.arange(0,1000):
# DRAW FROM THE GAUSSIAN: xis~N(mu,sig^2)
xis = mu + sig*np.random.randn(N,1);
xis = xis[ (xis<xmax) & (xis>xmin)] ;
# normalization for gaussian from 0..pi
normal = normfun(np.pi)-normfun(0) # 注意:概率密度函数在采样区间[0 pi]上的积分需要等于1
Iis[k] =np.mean(f(xis)/p(xis))*normal # 因此,此处需要乘一个系数即p(x)在[0 pi]上的积分
plt.subplot(1,2,2)
plt.hist(Iis,30, histtype='step', label=u'Importance Sampling');
plt.hist(Ivmc, 30, color='r',histtype='step', label=u'Vanilla MC');
plt.vlines(np.pi, 0, 100, color='g', linestyle='dashed')
plt.legend()
plt.show()
从图中可以看出曲线sin(x)*x的形状和正态分布曲线的形状相近,因此在曲线峰值处的采样点数目会比曲线上位置低的地方要多。精确计算的结果为pi,从上面的右图中可以看出:两种方法均计算定积分1000次,靠近精确值pi=3.1415处的结果最多,离精确值越远数目越少,显然这符合常规。但是采用传统方法(红色直方图)计算出的积分值方的差明显比采用重要抽样法(蓝色直方图)要大。因此,采用重要抽样法计算可以降低方差,提高精度。另外需要注意的是:关于函数f(x)的选择会对计算结果的精度产生影响,当我们选择的函数f(x)与g(x)相差较大时,计算结果的方差也会加大。
相关推荐:
Python编程中NotImplementedError的使用方法_python
以上就是python编程通过蒙特卡洛法计算定积分详解的详细内容,更多请关注php中文网其它相关文章!

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号