Jacobian Matrixとは何ですか?
あなたの場所への最短ルートがGoogleマップによってどのように決定されるかを考えたことがありますか?または、ステアリングホイールを自動的に移動すると、スピンしたときに車両の動きに影響を与える方法を考えたことがありますか?まあ、それはすべてヤコビアのマトリックスに帰着します。 Jacobian Matrixは、ベクトル関数の部分誘導体のマトリックスです。ヤコビアン球状座標の変換は、ヤコビアンが最も一般的に使用される場所です。それは、分化におけるヤコビアン球体座標変換の変換のアイデアに対処します。この記事では、ヤコビアのマトリックスの数学的概念、その式、決定要因、および私たちが日常生活でどのように使用しているかについて説明します。
目次
- ヤコビアンとは何ですか?
- ヤコビアのマトリックスとは何ですか?
- Jacobian Matrixの数学的基礎
- ベクトル値関数と多変数計算
- 表記と寸法
- 幾何学的解釈
- ヤコビアンおよびヤコビアン機能の可逆性
- ヤコビアンの特性
- Jacobian Matrixの計算
- Jacobian Matrixの分析導出
- Jacobian Matrixの数値近似
- Jacobian Matrixの自動分化
- Pythonを使用したJacobianマトリックスと決定要因の計算
- Jacobian Matrixのアプリケーション
- 結論
- よくある質問
ヤコビアンとは何ですか?
Jacobian Matrixとその決定要因は、同じ数の変数を持つ有限数の関数に対して定義され、「Jacobian」と呼ばれます。ある変数のセットの変更が、異なるスペース間でマッピングする関数の別の変数セットにどのように影響するかを示します。
このシナリオでは、変数に関する同じ関数の最初の部分導関数が各行に見られます。マトリックスは、等しい数の行と列を持つ正方行列、または不均一な数の行と列の長方形の行列です。
例:逆さまのトレイルで山をトレッキングしている間、通常、方向と程度の急な速さがあります。あなたが山のどこにいても、ヤコビアンはあなたの登山がどれほど急で、どのように進んでいるかをあなたに伝えるあなたのガイドを持っているようなものです。
また読む:機械学習の背後にある数学 - あなたが知る必要があるコアの概念
ヤコビアのマトリックスとは何ですか?
現在、Jacobianマトリックスは、関数による入力ベクトルの出力ベクトルへの変換を示す部分的な導関数からなるマトリックスです。各出力がすべての入力変数に対してどのように変化するかを説明します。関数f:ℝⁿ→ℝᵐ総数m成分とn変数の総数がある場合、ヤコビアン式は次のように表現できます。
シンボリックヤコビアンマトリックス:
マトリックス([[2*x、-1]、[2*y、2*x]])
ヤコビアンでのポイント(2、3):
マトリックス([[4、-1]、[6、4]])
ヤコビアン(シンボリック)の決定要因:
4*x ** 2 2*y
ポイントでの決定要因(2、3):
22
ポイントの数値ヤコビアン(2、3):
<code>[[ 4.000001 -1. ] [ 6. 4. ]]</code>
ここで、ヤコビアン式は、ポイントの周りの関数にローカルな線形近似を与え、関数がどのように伸び、回転、変換されているかについて説明します。
Jacobian Matrixの数学的基礎
Jacobian Matrixを完全に理解するために、数学のさまざまな基盤について説明します。
1。ベクター値関数と多変数計算
基本的に、あるスペースから別のスペースにポイントをマッピングする関数を指します。これらの関数には、複数の入力に対応する複数の出力があります。このような関数は、流体のダイナミクスなどの実生活システムの基礎構造を提供します。
ヤコビアンは、線形代数と多変数計算を組み合わせます。スカラー誘導体は、単一変動機能の変化率について教えてくれます。また、マトリックス形式で提示された複数の入力と出力を使用した関数の変化率についても説明しています。
また読む:深い学習の旅を始めながら知っておくべき12マトリックス操作
2。表記と寸法
ヤコビ行列の構造とフォーマットは、変換の表現に関する重要な情報を説明しています。関数f:ℝⁿへの場合、「n」は入力と「m」出力を表しますが、ヤコビアンは「n」マトリックスによって「m」です。 Jacobian Matrixのエントリは、jᵢⱼ=∂fᵢ/∂xⱼを示します。I'th出力関数の表現は、j'th入力変数に対して変化します。
したがって、マトリックスの寸法は変換に影響します。 3Dスペースから2Dスペースまで、Jacobianは出力と列に等しい行を入力に等しくし、2*3マトリックスになります。
3。幾何学的解釈
ヤコビアンの機能的挙動は、代数の定義を備えた視覚的洞察も説明しています。次の解釈は、ヤコビのマトリックスが幾何学的な用語での機能の局所的な挙動をどのように説明するかを特定するのに役立ちます。

- 局所線形変換:ヤコビアンは、ポイントの近傍で最も線形近似を機能させます。入力ポイントに関する無限に小さな領域が出力1にどのようにマップされるかを説明します。
- 接線近似:ヤコビアンは、入力空間から出力空間に接続されたベクトルを翻訳します。表面と考えると、これらの表面が互いにどのように回転するかについてのローカルな説明を提供します。
4.ヤコビアンおよびヤコビアン機能の可逆性
ヤコビアンと可逆性の関係は、必要な情報を証明しました。特定の時点での関数の局所的な動作に関する洞察を提供しました。

- | j | > 0:ローカルオリエンテーションは関数によって保存されます。
- | j |
- | j | = 0:特定の臨界点での可逆性が失われます
関数は、ヤコビアンが非弦楽器であるときはいつでも近隣で反転可能であると言われており、その決定要因はゼロに等しくありません。次に、その点と一致して、逆関数定理があります。しかし、ヤコビの決定要因がゼロになると、出力ドメインは折りたたみ、圧縮、または局在化を受けます。
また読む:データ科学者向けの線形代数の包括的な初心者ガイド
ヤコビアンの特性
それでは、ヤコビアンの特性を理解しましょう。
- チェーンルール:複合関数の場合、ヤコビアンを乗算して組成のヤコビアンを得ることができます。
- 方向誘導体:ヤコビアンを使用して、あらゆる方向に沿って方向微分を計算できます。
- 線形近似:任意の点近くの関数の近似は、f(xΔx)≈f(x)j(x)・Δxによって与えられます。
Jacobian Matrixの計算
ここで、ヤコビアのマトリックスを計算し、ヤコビアン球状座標の変換 - 分析派生、数値近似、自動分化の3つの異なる方法が表示されます。
Jacobian Matrixの分析導出
これは、部分的な導関数の直接計算に依存して、変換構造に関する洞察を提供するヤコビアンマトリックスを生成する古典的な方法です。各入力変数に対して各コンポーネント関数を体系的に区別することによって達成されます。
コンポーネントf₁、f₂、…、fₘ、および変数x₁、x₂、…、xₙを備えたベクトル関数f:ℝⁿ→ℝᵐが、各j = 1,2、….n。
j(x)= [<br> ∂f₁/∂x₁∂f₁/∂x₂...∂f₁/∂xₙ<br> ∂f₂/∂x₁∂f₂/∂x₂...∂f₂/∂xₙ<br> ... ... ... ...<br> ∂fₘ/∂x₁∂fₘ/∂x₂...∂fₘ/∂xₙ<br> ]<br><br>例:f(x、y)=(x²-y、2xy)、評価された部分的な導関数は次のとおりです。<br><br> ∂f₁/∂x= 2x<br> ∂f₁/∂y= -1<br> ∂f₂/∂x= 2y<br> ∂f₂/∂y= 2x<br><br>これにより、観察されたヤコビアのマトリックスは次のとおりです。<br><br> j(x、y)= [2x -1<br> 2y 2x]
この方法では、正確な結果を見ることができます。ただし、一度に複数の変数を処理したり、計算が不可能な複雑な機能を扱ったりして、物事は複雑になる可能性があります。
Jacobian Matrixの数値近似
分析派生が実行するにはかさばりすぎたり、関数にフォーム式がない場合はいつでも、数値的手法は、有限の違いを使用して部分的なデリバティブを計算する実用的な代替ソリューションを提供します。 2つの主要な有限差分方法は次のとおりです。
- フォワードの違い:
∂fi/∂xⱼ≈[f(x₁、...、xⱼh、...、xₙ)-f(x₁、...、xⱼ、...、xₙ)]/h
- より高い精度で中心的な違い
∂fi/∂xⱼⱼ≈[f(x₁、...、xⱼh、...、xₙ)-f(x₁、...、xⱼ -h、...、xₙ)]/(2h)
ここでは、h = 2倍の精度の場合、通常は10°である小さなステップです。
それはすべて、適切なサイズのステップを選択することです。大きすぎると近似誤差が発生しますが、小さい場合は変動点の制限のために数値の不安定性が発生します。適応段階のステップサイジングまたはリチャードソンの外挿を使用した高度な手法は、精度をさらに改善する可能性があります。
Jacobian Matrixの自動分化
分析の精度と計算自動化を組み合わせた自動差別化は、リストで非常に高くなります。 ADは、離散化の誤差を回避することにつながるのではなく、ADが正確なデリバティブを計算するのではなく、正確なデリバティブを計算するという点で数値的な方法とは異なります。自動分化の基礎原則は次のとおりです。
- チェーンルールの適用:関数を構成する基本操作のチェーンルールを体系的に適用します。
- 計算グラフの表現:関数は、既知の誘導体を伴う原始操作の尖ったグラフに分解されます。
- フォワードノードとリバースノード:フォワードモードは派生物を入力から出力へと伝播し、リバースモードは出力から入力への導関数を伝播します。

これにより、Tensorflow、Pytorch、Jaxなどの最新のソフトウェアフレームワークにとって、自動分化が非常にアクセスしやすく、効率的になります。彼らは、機械学習でヤコビアンを計算し、科学的なものとの最適化の問題を計算するためにそれを好みます。
Pythonを使用したJacobianマトリックスと決定要因の計算
Pythonを使用してヤコビアのマトリックスとヤコビアンの球状座標を実装する方法を見てみましょう。それぞれSympyとNumpyを使用して、シンボリック計算と数値近似の両方を使用します。
ステップ1:環境をセットアップします
関数を実行するために必要なパスをインポートします。
npとしてnumpyをインポートします sympyをsp pltとしてmatplotlib.pyplotをインポートします Matplotlib.Patchesからインポート楕円を
ステップ2:シンボリック計算を実行します
Sympyでシンボリック計算のための関数を書きます。
def symbolic_jacobian(): x、y = sp.symbols( 'x y') f1 = x ** 2 -y f2 = 2*x*y #関数ベクトルを定義します f = sp.matrix([f1、f2]) x = sp.matrix([x、y]) #ジャコビアンマトリックスを計算します j = f.jacobian(x) print( "Symbolic Jacobian Matrix:") 印刷(j) #ポイントでヤコビアンを計算する(2、3) j_at_point = j.subs([(x、2)、(y、3)]) print( "\ njacobian at Point(2、3):") 印刷(j_at_point) #決定要因を計算します det_j = j.det() print( "\ ndeterminant of Jacobian(Symbolic):") 印刷(det_j) print( "\ ndeTerminant at Point(2、3):") print(det_j.subs([(x、2)、(y、3)])) j、det_jを返します
ステップ3:数値近似を追加します
数値近似の関数をnumpyで書き込みます。
def numerical_jacobian(func、x、epsilon = 1e-6):
n = len(x)#入力変数の数
m = len(func(x))#出力変数の数
jacobian = np.zeros((m、n))
範囲(n)のiの場合:
x_plus = x.copy()
x_plus [i] = epsilon
jacobian [:、i] =(func(x_plus) - func(x)) / epsilon
ヤコビアンを返しますステップ4:実行機能を書きます
上記の関数の実行と変換の視覚化のための主な関数を記述します。
def f(x):
np.arrayを返す([x [0] ** 2 -x [1]、2*x [0]*x [1]])
#変換を視覚化します
def Visualize_transformation():
#ポイントのグリッドを作成します
x = np.linspace(-3、3、20)
y = np.linspace(-3、3、20)
x、y = np.meshgrid(x、y)
#変換されたポイントを計算します
u = x ** 2 -y
v = 2*x*y
#オリジナルと変換されたグリッドをプロットします
図、(ax1、ax2)= plt.subplots(1、2、figsize =(12、6))
#元のグリッド
ax1.set_title( 'オリジナルスペース')
ax1.set_xlabel( 'x')
ax1.set_ylabel( 'y')
ax1.grid(true)
ax1.plot(x、y、 'k。、markersize = 2)
#単位円を追加します
circle = plt.circle((0、0)、1、fill = false、color = 'red'、linewidth = 2)
ax1.add_artist(circle)
ax1.set_xlim(-3、3)
ax1.set_ylim(-3、3)
ax1.set_aspect( 'equal')
#変換されたグリッド
ax2.set_title( '変換されたスペース')
ax2.set_xlabel( 'u')
ax2.set_ylabel( 'v')
ax2.grid(true)
ax2.plot(u、v、 'k。、markersize = 2)
#単位円の変換を計算します
theta = np.linspace(0、2*np.pi、100)
x_circle = np.cos(theta)
y_circle = np.sin(theta)
u_circle = x_circle ** 2 -y_circle
v_circle = 2*x_circle*y_circle
ax2.plot(u_circle、v_circle、 'r-'、linewidth = 2)
#ポイント(1、0)に局所線形近似を表示します
point = np.array([1、0])
j = numerical_jacobian(f、point)
#私たちのポイントでヤコビアンが小さな円をどのように変換するかを計算します
スケール= 0.5
transformed_points = []
thetaのtの場合:
delta = scale * np.array([np.cos(t)、np.sin(t)])
transformed_delta = j @ delta
transformed_points.append(transformed_delta)
transformed_points = np.array(transformed_points)
#近似をプロットします
base_point_transformed = f(point)
ax2.plot(base_point_transformed [0] transformed_points [:、0]、
base_point_transformed [1] transformed_points [:, 1]、
'g-'、linewidth = 2、label = '線形近似')
ax2.legend()
plt.tight_layout()
plt.show()
#関数を実行します
symbolic_result = symbolic_jacobian()
point = np.array([2.0、3.0])
numerical_result = numerical_jacobian(f、point)
print( "\ nnumerical Jacobian at Point(2、3):")
print(numerical_result)
#変換を視覚化します
visualize_transformation()
出力:


出力レビュー:
非線形マッピングf(x、y)=(x²-y、2xy)が提案されており、ヤコビの特性が強調表示されます。元のスペースは左に均一なグリッドとユニット円で表示されますが、右のマップは変換後の空間を示しています。
ヤコビのマトリックスは、象徴的に([[2x、-1]、[2y、2*x]]))と数値ポイント(2,3)の両方で計算されます。これは、22に等しい決定要因を示します。これは、局所的に広い面積を意味します。したがって、この分析は、変換がどのように領域を歪めるかについての数学的な見解を提供します。線形化(緑の曲線)は、この非線形マッピングの局所構造を表します。
Jacobian Matrixのアプリケーション
最新のMLフレームワークには、Jacobianマトリックスを計算する自動分化ツールが含まれています。これは、次のような複雑なアプリケーションのゲームチェンジャーです。
- ロボットアームによる速度制御
- 動的システムの安定性分析:
- ヘビロボット障害物ナビゲーション:
- マニピュレーターのモーション計画:
- ロボット工学におけるフォーストルク変換:
結論
微積分学、差動幾何学、および線形代数はすべて、ヤコビのマトリックスが結びつき、実際のアプリケーションに適用する数学の分野です。高度な手術ロボットからGPSの場所まで、ヤコビアンは技術をより反応性と先天的にする上で大きな役割を果たしています。これは、数学がどのように私たちの宇宙を説明し、より効果的かつ効率的に対話するのに役立つかの例です。
よくある質問
Q1。ヤコビアンの決定要因とヤコビアンの完全なマトリックスをいつ使用しますか?A.決定要因は、ボリュームの変化と反転性に関する情報を提供しますが、完全なマトリックスは方向情報を提供します。スケーリング係数と可逆性を気にするときは、方向性の変換方法を知る必要がある場合は、完全なマトリックスを決定する場合は、決定要因を使用します。
Q2。ヤコビアンはどのように勾配と関係していますか?A.勾配は実際にはヤコビアンの特別なケースです!関数が1つの値(スカラーフィールド)のみを出力する場合、ヤコビアンは単一の行で、まさにその関数の勾配です。
Q3。ヤコビアンを計算できない場合はありますか?A.はい!あなたの関数がその時点で微分可能でない場合、ヤコビアンはそこで定義されていません。これは、関数のコーナー、カスプ、または不連続性で発生します。
Q4。ヤコビアンは座標変換でどのように使用されていますか?A.座標系(デカルトから極から極など)を変更すると、ヤコビアンは、システム間で領域またはボリュームがどのように変換されるかを決定します。これは、異なる座標系の積分を正しく計算するために、多変数計算で不可欠です。
Q5。数値エラーは、実際にヤコビアンの計算にどのように影響しますか?A.ヤコビアンの数値近似は、丸めのエラーと切り捨てエラーに苦しむ可能性があります。ロボット工学や財務モデリングなどの重要なアプリケーションでは、これらのエラーを最小限に抑えるために、自動分化などの洗練された手法がよく使用されます。
以上がJacobian Matrixとは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1669
1669
 14
14
 1428
1428
 52
52
 1329
1329
 25
25
 1273
1273
 29
29
 1256
1256
 24
24
 AGNOフレームワークを使用してマルチモーダルAIエージェントを構築する方法は?
Apr 23, 2025 am 11:30 AM
AGNOフレームワークを使用してマルチモーダルAIエージェントを構築する方法は?
Apr 23, 2025 am 11:30 AM
エージェントAIに取り組んでいる間、開発者は速度、柔軟性、リソース効率の間のトレードオフをナビゲートすることがよくあります。私はエージェントAIフレームワークを探索していて、Agnoに出会いました(以前はPhi-でした。
 SQLに列を追加する方法は? - 分析Vidhya
Apr 17, 2025 am 11:43 AM
SQLに列を追加する方法は? - 分析Vidhya
Apr 17, 2025 am 11:43 AM
SQLの変更テーブルステートメント:データベースに列を動的に追加する データ管理では、SQLの適応性が重要です。 その場でデータベース構造を調整する必要がありますか? Alter Tableステートメントはあなたの解決策です。このガイドの詳細は、コルを追加します
 ラマドラマを超えて:大規模な言語モデル用の4つの新しいベンチマーク
Apr 14, 2025 am 11:09 AM
ラマドラマを超えて:大規模な言語モデル用の4つの新しいベンチマーク
Apr 14, 2025 am 11:09 AM
問題のあるベンチマーク:ラマのケーススタディ 2025年4月上旬、MetaはLlama 4スイートのモデルを発表し、GPT-4oやClaude 3.5 Sonnetなどの競合他社に対して好意的に位置付けた印象的なパフォーマンスメトリックを誇っています。ラウンクの中心
 OpenaiはGPT-4.1でフォーカスをシフトし、コーディングとコスト効率を優先します
Apr 16, 2025 am 11:37 AM
OpenaiはGPT-4.1でフォーカスをシフトし、コーディングとコスト効率を優先します
Apr 16, 2025 am 11:37 AM
このリリースには、GPT-4.1、GPT-4.1 MINI、およびGPT-4.1 NANOの3つの異なるモデルが含まれており、大規模な言語モデルのランドスケープ内のタスク固有の最適化への動きを示しています。これらのモデルは、ようなユーザー向けインターフェイスをすぐに置き換えません
 ADHDゲーム、ヘルスツール、AIチャットボットがグローバルヘルスを変える方法
Apr 14, 2025 am 11:27 AM
ADHDゲーム、ヘルスツール、AIチャットボットがグローバルヘルスを変える方法
Apr 14, 2025 am 11:27 AM
ビデオゲームは不安を緩和したり、ADHDの子供を焦点を合わせたり、サポートしたりできますか? ヘルスケアの課題が世界的に急増しているため、特に若者の間では、イノベーターはありそうもないツールであるビデオゲームに目を向けています。現在、世界最大のエンターテイメントインダスの1つです
 Andrew Ngによる埋め込みモデルに関する新しいショートコース
Apr 15, 2025 am 11:32 AM
Andrew Ngによる埋め込みモデルに関する新しいショートコース
Apr 15, 2025 am 11:32 AM
埋め込みモデルのパワーのロックを解除する:Andrew Ngの新しいコースに深く飛び込む マシンがあなたの質問を完全に正確に理解し、応答する未来を想像してください。 これはサイエンスフィクションではありません。 AIの進歩のおかげで、それはRになりつつあります
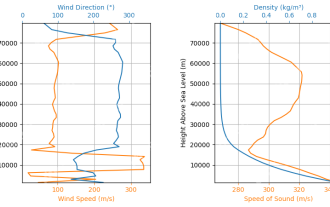 Rocketpyを使用したロケットの起動シミュレーションと分析-AnalyticsVidhya
Apr 19, 2025 am 11:12 AM
Rocketpyを使用したロケットの起動シミュレーションと分析-AnalyticsVidhya
Apr 19, 2025 am 11:12 AM
Rocketpy:A包括的なガイドでロケット発売をシミュレートします この記事では、強力なPythonライブラリであるRocketpyを使用して、高出力ロケット発売をシミュレートすることをガイドします。 ロケットコンポーネントの定義からシミュラの分析まで、すべてをカバーします
 Googleは、次の2025年にクラウドで最も包括的なエージェント戦略を発表します
Apr 15, 2025 am 11:14 AM
Googleは、次の2025年にクラウドで最も包括的なエージェント戦略を発表します
Apr 15, 2025 am 11:14 AM
GoogleのAI戦略の基礎としてのGemini Geminiは、GoogleのAIエージェント戦略の基礎であり、高度なマルチモーダル機能を活用して、テキスト、画像、オーディオ、ビデオ、コード全体で応答を処理および生成します。 DeepMによって開発されました




