The Unreasonable Usefulness of numpy&#s einsum
Introduction
I'd like to introduce you to the most useful method in Python, np.einsum.
With np.einsum (and its counterparts in Tensorflow and JAX), you can write complicated matrix and tensor operations in an extremely clear and succinct way. I've also found that its clarity and succinctness relieves a lot of the mental overload that comes with working with tensors.
And it's actually fairly simple to learn and use. Here's how it works:
In np.einsum, you have a subscripts string argument and you have one or more operands:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
The subscripts argument is a "mini-language" that tells numpy how to manipulate and combine the axes of the operands. It's a little difficult to read at first, but it's not bad when you get the hang of it.
Single Operands
For a first example, let's use np.einsum to swap the axes of (a.k.a. take the transpose) a matrix A:
M = np.einsum('ij->ji', A)
The letters i and j are bound to the first and second axes of A. Numpy binds letters to axes in the order they appear, but numpy doesn't care what letters you use if you are explicit. We could have used a and b, for example, and it works the same way:
M = np.einsum('ab->ba', A)
However, you must supply as many letters as there are axes in the operand. There are two axes in A, so you must supply two distinct letters. The next example won't work because the subscripts formula only has one letter to bind, i:
# broken
M = np.einsum('i->i', A)
On the other hand, if the operand does indeed have only one axis (i.o.w., it is a vector), then the single-letter subscript formula works just fine, although it isn't very useful because it leaves the vector a as-is:
m = np.einsum('i->i', a)
Summing Over Axes
But what about this operation? There's no i on the right-hand-side. Is this valid?
c = np.einsum('i->', a)
Surprisingly, yes!
Here is the first key to understanding the essence of np.einsum: If an axis is omitted from the right-hand-side, then the axis is summed over.

Code:
c = 0 I = len(a) for i in range(I): c += a[i]
The summing-over behavior isn't limited to a single axis. For example, you can sum over two axes at once by using this subscript formula: c = np.einsum('ij->', A):

Here is the corresponding Python code for something over both axes:
c = 0
I,J = A.shape
for i in range(I):
for j in range(J):
c += A[i,j]
But it doesn't stop there - we can get creative and sum some axes and leave others alone. For example: np.einsum('ij->i', A) sums the rows of matrix A, leaving a vector of row sums of length j:

Code:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
Likewise, np.einsum('ij->j', A) sums columns in A.

Code:
M = np.einsum('ij->ji', A)
Two Operands
There's a limit to what we can do with a single operand. Things get a lot more interesting (and useful) with two operands.
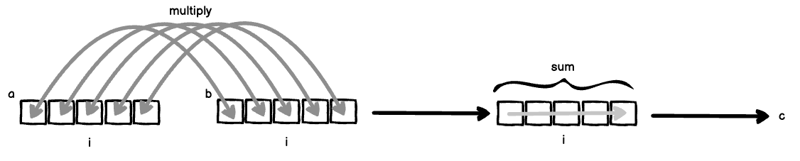
Let's suppose you have two vectors a = [a_1, a_2, ... ] and b = [a_1, a_2, ...].
If len(a) === len(b), we can compute the inner product (also called the dot product) like this:
M = np.einsum('ab->ba', A)
Two things are happening here simultaneously:
- Because i is bound to both a and b, a and b are "lined up" and then multiplied together: a[i] * b[i].
- Because the index i is excluded from the right-hand-side, axis i is summed over in order to eliminate it.
If you put (1) and (2) together, you get the classic inner product.
Code:
# broken
M = np.einsum('i->i', A)
Now, let's suppose that we didn't omit i from the subscript formula, we would multiply all a[i] and b[i] and not sum over i:
m = np.einsum('i->i', a)

Code:
c = np.einsum('i->', a)
This is also called element-wise multiplication (or the Hadamard Product for matrices), and is typically done via the numpy method np.multiply.
There's yet a third variation of the subscript formula, which is called the outer product.
c = 0 I = len(a) for i in range(I): c += a[i]
In this subscript formula, the axes of a and b are bound to separate letters, and thus are treated as separate "loop variables". Therefore C has entries a[i] * b[j] for all i and j, arranged into a matrix.

Code:
c = 0
I,J = A.shape
for i in range(I):
for j in range(J):
c += A[i,j]
Three Operands
Taking the outer product a step further, here's a three-operand version:
I,J = A.shape
r = np.zeros(I)
for i in range(I):
for j in range(J):
r[i] += A[i,j]

The equivalent Python code for our three-operand outer product is:
I,J = A.shape
r = np.zeros(J)
for i in range(I):
for j in range(J):
r[j] += A[i,j]
Going even further, there's nothing stopping us from omitting axes to sum over them in addition to transposing the result by writing ki instead of ik on the right-hand-side of ->:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
The equivalent Python code would read:
M = np.einsum('ij->ji', A)
Now I hope you can begin to see how you can specify complicated tensor operations rather easily. When I worked more extensively with numpy, I found myself reaching for np.einsum any time I had to implement a complicated tensor operation.
In my experience, np.einsum makes for easier code reading later - I can readily read off the above operation straight from the subscripts: "The outer product of three vectors, with the middle axes summed over, and the final result transposed". If I had to read a complicated series of numpy operations, I might find myself tongue tied.
A Practical Example
For a practical example, let's implement the equation at the heart of LLMs, from the classic paper "Attention is All You Need".
Eq. 1 describes the Attention Mechanism:

We'll focus our attention on the term QKT , because softmax isn't computible by np.einsum and the scaling factor dk1 is trivial to apply.
The QKT term represents the dot products of m queries with n keys. Q is a collection of m d-dimensional row vectors stacked into a matrix, so Q has the shape md. Likewise, K is a collection of n d-dimensional row vectors stacked into a matrix, so K has the shape md.
The product between a single Q and K would be written as:
np.einsum('md,nd->mn', Q, K)
Note that because of the way we wrote our subscripts equation, we avoided having to transpose K prior to matrix multiplication!

So, that seems pretty straightforward - in fact, it's just a traditional matrix multiplication. However, we're not done yet. Attention Is All You Need uses multi-head attention, which means we really have k such matrix multiplies happening simultaneously over an indexed collection of Q matrices and K matrices.
To make things a bit clearer, we might rewrite the product as QiKiT .
That means we have an additional axis i for both Q and K.
And what's more, if we are in a training setting, we are probably executing a batch of such multi-headed attention operations.
So presumably would want to perform the operation over a batch of examples along a batch axis b. Thus, the complete product would be something like:
numpy.einsum(subscripts : string, *operands : List[np.ndarray])
I'm going to skip the diagram here because we're dealing with 4-axis tensors. But you might be able to picture "stacking" the earlier diagram to get our multi-head axis i, and then "stacking" those "stacks" to get our batch axis b.
It's difficult for me to see how we would implement such an operation with any combination of the other numpy methods. Yet, with a little bit of inspection, it's clear what's happening: Over a batch, over a collection of matrices Q and K, perform the matrix multiplication Qt(K).
Now, isn't that wonderful?
Shameless Plug
After doing the founder mode grind for a year, I'm looking for work. I've got over 15 years experience in a wide variety of technical fields and programming languages and also experience managing teams. Math and statistics are focus areas. DM me and let's talk!
The above is the detailed content of The Unreasonable Usefulness of numpy&#s einsum. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1670
1670
 14
14
 1428
1428
 52
52
 1329
1329
 25
25
 1274
1274
 29
29
 1256
1256
 24
24
 Python vs. C : Learning Curves and Ease of Use
Apr 19, 2025 am 12:20 AM
Python vs. C : Learning Curves and Ease of Use
Apr 19, 2025 am 12:20 AM
Python is easier to learn and use, while C is more powerful but complex. 1. Python syntax is concise and suitable for beginners. Dynamic typing and automatic memory management make it easy to use, but may cause runtime errors. 2.C provides low-level control and advanced features, suitable for high-performance applications, but has a high learning threshold and requires manual memory and type safety management.
 Python and Time: Making the Most of Your Study Time
Apr 14, 2025 am 12:02 AM
Python and Time: Making the Most of Your Study Time
Apr 14, 2025 am 12:02 AM
To maximize the efficiency of learning Python in a limited time, you can use Python's datetime, time, and schedule modules. 1. The datetime module is used to record and plan learning time. 2. The time module helps to set study and rest time. 3. The schedule module automatically arranges weekly learning tasks.
 Python vs. C : Exploring Performance and Efficiency
Apr 18, 2025 am 12:20 AM
Python vs. C : Exploring Performance and Efficiency
Apr 18, 2025 am 12:20 AM
Python is better than C in development efficiency, but C is higher in execution performance. 1. Python's concise syntax and rich libraries improve development efficiency. 2.C's compilation-type characteristics and hardware control improve execution performance. When making a choice, you need to weigh the development speed and execution efficiency based on project needs.
 Learning Python: Is 2 Hours of Daily Study Sufficient?
Apr 18, 2025 am 12:22 AM
Learning Python: Is 2 Hours of Daily Study Sufficient?
Apr 18, 2025 am 12:22 AM
Is it enough to learn Python for two hours a day? It depends on your goals and learning methods. 1) Develop a clear learning plan, 2) Select appropriate learning resources and methods, 3) Practice and review and consolidate hands-on practice and review and consolidate, and you can gradually master the basic knowledge and advanced functions of Python during this period.
 Python vs. C : Understanding the Key Differences
Apr 21, 2025 am 12:18 AM
Python vs. C : Understanding the Key Differences
Apr 21, 2025 am 12:18 AM
Python and C each have their own advantages, and the choice should be based on project requirements. 1) Python is suitable for rapid development and data processing due to its concise syntax and dynamic typing. 2)C is suitable for high performance and system programming due to its static typing and manual memory management.
 Which is part of the Python standard library: lists or arrays?
Apr 27, 2025 am 12:03 AM
Which is part of the Python standard library: lists or arrays?
Apr 27, 2025 am 12:03 AM
Pythonlistsarepartofthestandardlibrary,whilearraysarenot.Listsarebuilt-in,versatile,andusedforstoringcollections,whereasarraysareprovidedbythearraymoduleandlesscommonlyusedduetolimitedfunctionality.
 Python: Automation, Scripting, and Task Management
Apr 16, 2025 am 12:14 AM
Python: Automation, Scripting, and Task Management
Apr 16, 2025 am 12:14 AM
Python excels in automation, scripting, and task management. 1) Automation: File backup is realized through standard libraries such as os and shutil. 2) Script writing: Use the psutil library to monitor system resources. 3) Task management: Use the schedule library to schedule tasks. Python's ease of use and rich library support makes it the preferred tool in these areas.
 Python for Web Development: Key Applications
Apr 18, 2025 am 12:20 AM
Python for Web Development: Key Applications
Apr 18, 2025 am 12:20 AM
Key applications of Python in web development include the use of Django and Flask frameworks, API development, data analysis and visualization, machine learning and AI, and performance optimization. 1. Django and Flask framework: Django is suitable for rapid development of complex applications, and Flask is suitable for small or highly customized projects. 2. API development: Use Flask or DjangoRESTFramework to build RESTfulAPI. 3. Data analysis and visualization: Use Python to process data and display it through the web interface. 4. Machine Learning and AI: Python is used to build intelligent web applications. 5. Performance optimization: optimized through asynchronous programming, caching and code




