 Backend-Entwicklung
Backend-Entwicklung
 PHP-Tutorial
PHP-Tutorial
 Finden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume
Finden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume
Finden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume
3203. Finden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume
Schwierigkeit:Schwer
Themen: Baum, Tiefensuche, Breitensuche, Diagramm
Es gibt zwei ungerichtete Bäume mit n und m Knoten, nummeriert von 0 bis n - 1 bzw. von 0 bis m - 1. Sie erhalten zwei 2D-Integer-Arrays „Kanten1“ und „Kanten2“ mit den Längen n – 1 bzw. m – 1, wobei „Kanten1[i] = [ai, bi]“ darauf hinweist ist eine Kante zwischen den Knoten ai und bi im ersten Baum und Kanten2[i] = [ui, vi] zeigt an, dass es eine Kante zwischen den Knoten ui und vi im zweiten Baum gibt.
Sie müssen einen Knoten aus dem ersten Baum mit einem anderen Knoten aus dem zweiten Baum über eine Kante verbinden.
Gib den minimalstenmöglichen Durchmesser des resultierenden Baums zurück.
Der Durchmesser eines Baumes ist die Länge des längsten Pfades zwischen zwei beliebigen Knoten im Baum.
Beispiel 1:
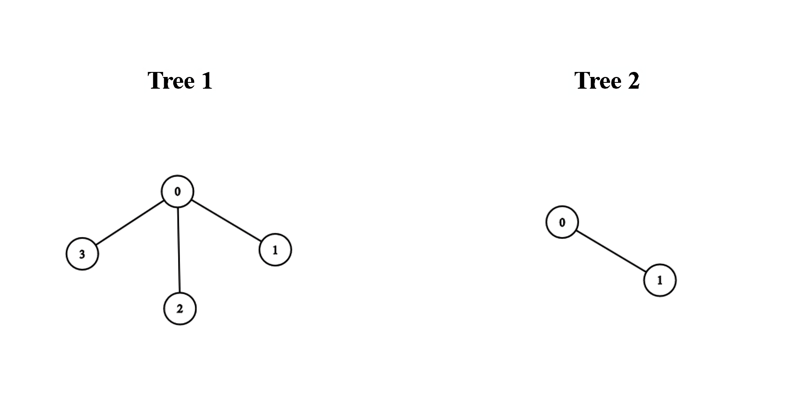
- Eingabe: Kanten1 = [[0,1],[0,2],[0,3]], Kanten2 = [[0,1]]
- Ausgabe: 3
- Erklärung: Wir können einen Baum mit einem Durchmesser von 3 erhalten, indem wir Knoten 0 des ersten Baums mit einem beliebigen Knoten des zweiten Baums verbinden.
Beispiel 2:
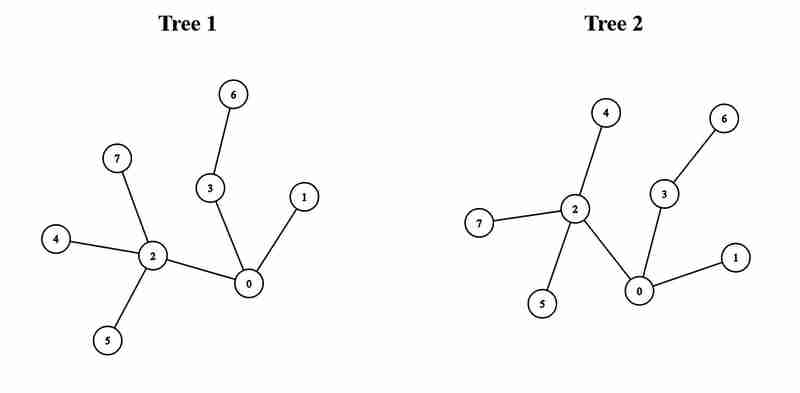
- Eingabe: Kanten1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2, 7]], Kanten2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
- Ausgabe: 5
- Erklärung: Wir können einen Baum mit einem Durchmesser von 5 erhalten, indem wir Knoten 0 des ersten Baums mit Knoten 0 des zweiten Baums verbinden.
Einschränkungen:
- 1 <= n, m <= 105
- edges1.length == n - 1
- edges2.length == m - 1
- Kanten1[i].länge == Kanten2[i].länge == 2
- Kanten1[i] = [ai, bi]
- 0 <= ai, bi < n
- Kanten2[i] = [ui, vi]
- 0 <= ui, vi < m
- Die Eingabe wird so generiert, dass Kanten1 und Kanten2 gültige Bäume darstellen.
Hinweis:
- Angenommen, wir haben Knoten a in Baum1 mit Knoten b in Baum2 verbunden. Die Durchmesserlänge des resultierenden Baums ist der größte der folgenden drei Werte:
- Der Durchmesser von Baum 1.
- Der Durchmesser von Baum 2.
- Die Länge des längsten Pfads, der bei Knoten a beginnt und vollständig innerhalb von Baum 1 liegt. Die Länge des längsten Pfads, der bei Knoten b beginnt und vollständig innerhalb von Baum 2 liegt 1.
- Der hinzugefügte Wert im dritten Wert ist auf die zusätzliche Kante zurückzuführen, die wir zwischen den Bäumen 1 und 2 hinzugefügt haben.
- Die Werte 1 und 2 sind unabhängig von unserer Wahl von a und b konstant. Daher müssen wir a und b so auswählen, dass der Wert 3 minimiert wird.
- Wenn wir a und b optimal auswählen, haben sie jeweils die Durchmesser von Baum 1 und Baum 2. Welche Knoten des Durchmessers sollten wir genau auswählen?
- a ist der Mittelpunkt des Durchmessers von Baum 1 und b ist der Mittelpunkt des Durchmessers von Baum 2.
Lösung:
Wir müssen Schritt für Schritt vorgehen und uns dabei darauf konzentrieren, zu verstehen, wie der Durchmesser eines Baumes berechnet wird und wie sich die Verbindung der beiden Bäume auf den Gesamtdurchmesser auswirkt.
Lösungsschritte:
-
Ermitteln Sie den Durchmesser jedes Baumes:
- Der Durchmesser eines Baumes ist der längste Weg zwischen zwei beliebigen Knoten. Um es zu finden, können wir den folgenden zweistufigen Prozess verwenden:
- Führen Sie ein BFS (oder DFS) von einem beliebigen Knoten aus durch, um den am weitesten entfernten Knoten zu finden (nennen wir diesen Knoten A).
- Führen Sie ein weiteres BFS (oder DFS) beginnend bei A durch, um den am weitesten von A entfernten Knoten zu finden (nennen wir diesen Knoten B), und der Abstand von A nach B entspricht dem Durchmesser des Baums.
- Der Durchmesser eines Baumes ist der längste Weg zwischen zwei beliebigen Knoten. Um es zu finden, können wir den folgenden zweistufigen Prozess verwenden:
-
Bestimmen Sie die optimalen Knoten zum Verbinden:
- Aus dem Hinweis in der Aufgabe geht hervor, dass der beste Weg, den zusätzlichen Durchmesser beim Verbinden zweier Bäume zu minimieren, darin besteht, die Mittelpunkte der Durchmesser beider Bäume zu verbinden. Dadurch wird der längste Weg minimiert, der durch die neue Kante verursacht wird.
- Der optimale Knoten im Durchmesser eines Baumes ist normalerweise die „Mitte“, die gefunden werden kann, indem eine BFS von den Endpunkten des Durchmessers aus durchgeführt und die Mitte des längsten Pfads ermittelt wird.
-
Gesamtdurchmesser minimieren:
- Sobald wir die Mittelpunkte beider Bäume gefunden haben, ist der neue Durchmesser das Maximum von:
- Der Durchmesser von Baum 1.
- Der Durchmesser von Baum 2.
- Die Summe aus dem längsten Pfad in Baum 1, dem längsten Pfad in Baum 2 und 1 für die neue Verbindungskante.
- Sobald wir die Mittelpunkte beider Bäume gefunden haben, ist der neue Durchmesser das Maximum von:
Lassen Sie uns diese Lösung in PHP implementieren: 3203. Finden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume
Erläuterung:
BFS-Hilfsfunktion: Die BFS-Funktion berechnet den am weitesten von einem bestimmten Startknoten entfernten Knoten und gibt das Distanzarray und den am weitesten entfernten gefundenen Knoten zurück. Dies ist wichtig für die Berechnung des Baumdurchmessers.
Durchmesser und Mittelpunkt abrufen: Die Funktion getDiameterAndCenter ermittelt den Durchmesser eines Baums und seinen Mittelpunkt. Die Mitte des Baumes ist entscheidend für die Minimierung des Durchmessers des neuen Baumes beim Zusammenführen zweier Bäume.
Hauptlösung:
- Wir erstellen zunächst Adjazenzlisten für beide Bäume.
- Wir berechnen den Durchmesser und die Mitte für beide Bäume.
- Wir führen BFS von den Zentren beider Bäume aus durch, um die längsten Pfade innerhalb jedes Baums zu erhalten.
- Zuletzt berechnen wir das Maximum der drei Werte, um den minimalen Durchmesser des zusammengeführten Baums zu erhalten.
Zeitkomplexität:
- Erstellen der Adjazenzliste: O(n m)
- BFS-Durchquerung: O(n m)
- Die Gesamtzeitkomplexität beträgt O(n m), was für die Eingabegrößenbeschränkung von 105 effizient ist.
Dieser Ansatz stellt sicher, dass wir beim Zusammenführen der beiden Bäume den minimal möglichen Durchmesser finden.
Kontaktlinks
Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, dem Repository einen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!
Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:
- GitHub
Das obige ist der detaillierte Inhalt vonFinden Sie den Mindestdurchmesser nach dem Zusammenführen zweier Bäume. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1676
1676
 14
14
 1429
1429
 52
52
 1333
1333
 25
25
 1278
1278
 29
29
 1257
1257
 24
24
 Erklären Sie sicheres Kennwort -Hashing in PHP (z. B. password_hash, password_verify). Warum nicht MD5 oder SHA1 verwenden?
Apr 17, 2025 am 12:06 AM
Erklären Sie sicheres Kennwort -Hashing in PHP (z. B. password_hash, password_verify). Warum nicht MD5 oder SHA1 verwenden?
Apr 17, 2025 am 12:06 AM
In PHP sollten die Funktionen für Passwort_Hash und passwart_verify verwendet werden, um sicheres Passwort -Hashing zu implementieren, und MD5 oder SHA1 sollte nicht verwendet werden. 1) Passwort_hash generiert einen Hash, der Salzwerte enthält, um die Sicherheit zu verbessern. 2) Passwort_Verify prüfen Sie das Passwort und sicherstellen Sie die Sicherheit, indem Sie die Hash -Werte vergleichen. 3) MD5 und SHA1 sind anfällig und fehlen Salzwerte und sind nicht für die Sicherheit der modernen Passwort geeignet.
 Wie funktioniert der Php -Typ -Hinweis, einschließlich Skalartypen, Rückgabetypen, Gewerkschaftstypen und nullbaren Typen?
Apr 17, 2025 am 12:25 AM
Wie funktioniert der Php -Typ -Hinweis, einschließlich Skalartypen, Rückgabetypen, Gewerkschaftstypen und nullbaren Typen?
Apr 17, 2025 am 12:25 AM
PHP -Typ -Eingabeaufforderungen zur Verbesserung der Codequalität und der Lesbarkeit. 1) Tipps zum Skalartyp: Da Php7.0 in den Funktionsparametern wie int, float usw. angegeben werden dürfen. 3) Eingabeaufforderung für Gewerkschaftstyp: Da Php8.0 in Funktionsparametern oder Rückgabetypen angegeben werden dürfen. 4) Nullierstyp Eingabeaufforderung: Ermöglicht die Einbeziehung von Nullwerten und Handlungsfunktionen, die Nullwerte zurückgeben können.
 PHP und Python: Verschiedene Paradigmen erklärt
Apr 18, 2025 am 12:26 AM
PHP und Python: Verschiedene Paradigmen erklärt
Apr 18, 2025 am 12:26 AM
PHP ist hauptsächlich prozedurale Programmierung, unterstützt aber auch die objektorientierte Programmierung (OOP). Python unterstützt eine Vielzahl von Paradigmen, einschließlich OOP, funktionaler und prozeduraler Programmierung. PHP ist für die Webentwicklung geeignet, und Python eignet sich für eine Vielzahl von Anwendungen wie Datenanalyse und maschinelles Lernen.
 PHP und Python: Code Beispiele und Vergleich
Apr 15, 2025 am 12:07 AM
PHP und Python: Code Beispiele und Vergleich
Apr 15, 2025 am 12:07 AM
PHP und Python haben ihre eigenen Vor- und Nachteile, und die Wahl hängt von den Projektbedürfnissen und persönlichen Vorlieben ab. 1.PHP eignet sich für eine schnelle Entwicklung und Wartung großer Webanwendungen. 2. Python dominiert das Gebiet der Datenwissenschaft und des maschinellen Lernens.
 Wie verhindern Sie die SQL -Injektion in PHP? (Vorbereitete Aussagen, PDO)
Apr 15, 2025 am 12:15 AM
Wie verhindern Sie die SQL -Injektion in PHP? (Vorbereitete Aussagen, PDO)
Apr 15, 2025 am 12:15 AM
Die Verwendung von Vorverarbeitungsanweisungen und PDO in PHP kann SQL -Injektionsangriffe effektiv verhindern. 1) Verwenden Sie PDO, um eine Verbindung zur Datenbank herzustellen und den Fehlermodus festzulegen. 2) Erstellen Sie Vorverarbeitungsanweisungen über die Vorbereitungsmethode und übergeben Sie Daten mit Platzhaltern und führen Sie Methoden aus. 3) Abfrageergebnisse verarbeiten und die Sicherheit und Leistung des Codes sicherstellen.
 PHP: Datenbanken und serverseitige Logik bearbeiten
Apr 15, 2025 am 12:15 AM
PHP: Datenbanken und serverseitige Logik bearbeiten
Apr 15, 2025 am 12:15 AM
PHP verwendet MySQLI- und PDO-Erweiterungen, um in Datenbankvorgängen und serverseitiger Logikverarbeitung zu interagieren und die serverseitige Logik durch Funktionen wie Sitzungsverwaltung zu verarbeiten. 1) Verwenden Sie MySQLI oder PDO, um eine Verbindung zur Datenbank herzustellen und SQL -Abfragen auszuführen. 2) Behandeln Sie HTTP -Anforderungen und Benutzerstatus über Sitzungsverwaltung und andere Funktionen. 3) Verwenden Sie Transaktionen, um die Atomizität von Datenbankvorgängen sicherzustellen. 4) Verhindern Sie die SQL -Injektion, verwenden Sie Ausnahmebehandlung und Schließen von Verbindungen zum Debuggen. 5) Optimieren Sie die Leistung durch Indexierung und Cache, schreiben Sie hochlesbarer Code und führen Sie die Fehlerbehandlung durch.
 Zweck von PHP: Erstellen dynamischer Websites
Apr 15, 2025 am 12:18 AM
Zweck von PHP: Erstellen dynamischer Websites
Apr 15, 2025 am 12:18 AM
PHP wird verwendet, um dynamische Websites zu erstellen. Zu den Kernfunktionen gehören: 1. Dynamische Inhalte generieren und Webseiten in Echtzeit generieren, indem Sie eine Verbindung mit der Datenbank herstellen; 2. Verarbeiten Sie Benutzerinteraktions- und Formulareinreichungen, überprüfen Sie Eingaben und reagieren Sie auf Operationen. 3. Verwalten Sie Sitzungen und Benutzerauthentifizierung, um eine personalisierte Erfahrung zu bieten. 4. Optimieren Sie die Leistung und befolgen Sie die Best Practices, um die Effizienz und Sicherheit der Website zu verbessern.
 Wählen Sie zwischen PHP und Python: Ein Leitfaden
Apr 18, 2025 am 12:24 AM
Wählen Sie zwischen PHP und Python: Ein Leitfaden
Apr 18, 2025 am 12:24 AM
PHP eignet sich für Webentwicklung und schnelles Prototyping, und Python eignet sich für Datenwissenschaft und maschinelles Lernen. 1.PHP wird für die dynamische Webentwicklung verwendet, mit einfacher Syntax und für schnelle Entwicklung geeignet. 2. Python hat eine kurze Syntax, ist für mehrere Felder geeignet und ein starkes Bibliotheksökosystem.



